12. UNIVERSUMI HORISONT
Universumil on kõigi Friedman´i mudelite korral horisont. Horisondist kaugemal toimuvad sündmused ei avalda meile mingit mõju ega ei ole avaldanud seda ka minevikus. Horisondi olemasolu järeldub kahest tõsiasjast:
a) kõigi Friedman´i mudelite korral on Universumil algus (sünnimoment minevikus);
b) ükski osake ega signaal ei saa liikuda valgusest kiiremini.
Vaatleja jaoks on olemas maksimaalne kaugus,
millest kaugemalt ei ole võimalik informatsiooni hankida. See kaugus on võrdne
teepikkusega, mille footon jõuab läbida Universumi ea jooksul. Universumi vananedes
kasvab horisondi kaugus 
võrdeliselt
Universumi vanusega t: 
Horisondi kaugus sõltub sellest, millisel
viisil viiakse läbi vastav mõõtmine. Näiteks mittefüüsikalise "mõõtmise"
korral, kus mõõtmine viiakse läbi hetkeliselt ajamomendil t horisonti
ja vaatlejat ühendava radiaalse sirge kõigis punktides, saame, tuginedes Robertson-Walker´i
meetrikale ja tabelile 1, tasases Friedman´i mudelis horisondi kauguseks
. Kauguste
ja 
kolmekordne
erinevus on tingitud asjaolust, et valgussignaali leviku kestel Universum paisub
ja objektid, kust signaalid kiirati, asuvad omaaja hetkel t vaatlejast
palju kaugemal kui kiirgamise momendil.
Lähemal vaatlusel järeldub, et horisondi poolt hõlmatav Universumi ruumiline piirkond kasvab ajas kiiremini kui Universum paisub - aja jooksul horisondi sisse jäävate galaktikate arv kasvab (vt joonis 7).
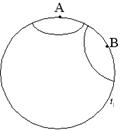
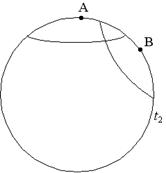
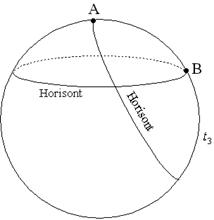
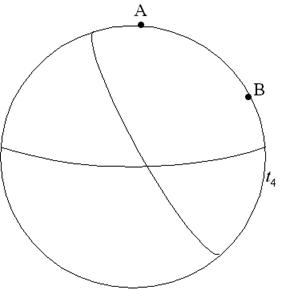
Joonis 7. Horisont paisuvas Universumis.
Siin on Universumit kujutatud
nelja sfäärina, neljal erineval ajahetkel 
. Vaatlejate
jaoks punktides A ja B asuvad horisondid kaugustel, millistest kaugemalt tulevad
valgussignaalid ei suuda jõuda vaatlejateni. Aja kasvades horisondi poolt hõlmatava
ruumiosa mõõtmed kasvavad kiiremini kui Universum paisub. Kuni ajamomendini
puudub vaatlejate
A ja B vahel põhjuslik side.
Veendumaks öeldus, leiame horisondi sisse jääva massi M sõltuvuse Universumi vanusest t, tuginedes tabelis 1 toodud andmetele. Asugu vaatleja ruumiliste koordinaatide alguspunktis. Astronoomiliste objektide arvu ja nende massi ajamomendil t määrab ta valguskiirusega levivate signaalide vahendusel (elektromagnetlained, neutriinod). Positiivse kõverusega ruumi korral avaldub horisondi sisse jääv registreeritav mass järgmiselt (vt valem (1.37)):
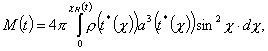
kus 
- on horisondi
radiaalne koordinaat ajamomendil t ja 
- ainetihedus
ajamomendil 
. Sümbol
rõhutab
asjaolu, et ajamoment 
sõltub
astronoomilise objekti radiaalkoordinaadist
- mida
suurem on , seda
kaugemal on objekt vaatlejast ja seda varem pidi signaal olema väljakiiratud,
et jõuda ajamomendiks t vaatlejani. Arvestades valemit
, saame:
 |
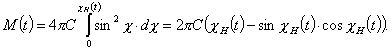(1.59) |
Horisondi radiaalkoordinaadi
leidmiseks
on otstarbekas kasutada aja parameetrilist esitust parameetri 
kaudu
(vt tabel 1).
Diferentseerimise teel veendume, et kõigi mudelite korral 
kehtib seos:
 . |
(1.60) |
Arvestades, et valguskiirusega leviva signaali
korral on 4-intervall 
, saame
valemitest (1.28) ja (1.29)
koordinaatide alguspunkti tuleva signaali jaoks:
 . |
(1.61) |
Võrdustest (1.59) ja (1.60) järeldub seos:
 . |
(1.62) |
Valemi (1.62) põhjal on lihtne veenduda, et
 . |
(1.63) |
Rõhutagem, et seosed (1.60),
(1.61) ja (1.63)
on õiged kõigi Friedman´i mudelite korral. Asendades horisondi radiaalkoordinaadi
avaldise võrdusesse (1.59), saame:
 ,
 , |
(1.64) |
kus 
on kinnise Universumi kogu mass. Kuna aeg
t kasvab monotoonselt kasvades
(vt tabel 1), siis piisab, kui vaatleme M käitumist
järgi.
Parameetri kasvades 0-st kuni 
-ni, horisondi
sisse jääv mass kasvab 0-st kuni -ni. See
tähendab, et horisondi paisumine on kiirem kui Universumi paisumine. Ajamomendil,
mil kinnine Universum hakkab uuesti kokku tõmbuma, hõlmab horisont kogu Universumi.
Parameetri edasisel
kasvamisel, on suuruse 
edasine
kasv fiktiivne, kuna kokkutõmbuvas Universumis kauged objektid registreeritakse
kahekordselt (kahest diametraalselt vastupidisest suunast). Valemist (1.64)
on näha, et kõik objektid Universumis on jälgitavad kahekordselt Universumi
"surma" momendil
. Seega
kinnises Universumis me iseennast seljatagant ei näe.
Negatiivse kõverusega Universumi puhul on horisondi sisse jääv mass määratud avaldisega:
 ,
 . |
(1.65) |
Mass kasvab
tõkestamatult "aja"
kasvades.
Seega ka 
korral
paisub horisont kiiremini kui Universum. Erinevalt positiivse kõverusega juhust
on siin kõik objektid jälgitavad ainult ühekordselt. Tasase mudeli korral
kehtib
 ,
 , |
(1.66) |
kus 
on konstant.
Kõik negatiivse kõverusega Universumi korral tehtud järeldused jäävad kehtima
ka juhul kui, 
Kõigil
mudelitel on veel üks oluline ühine joon. Universumi sünnimomendi läheduses,
kui t on väga väike, on horisondi poolt hõlmatav mass samuti väike (vt
valemeid (1.64), (1.65), (1.66)).
Niisiis võib järeldada, et mida varasemat aega vaatleme, seda vähem oluliseks osutub
Universumi kui terviku kõverus.
Selle asjaolu tõttu saame anda võrdlemisi selge pildi Universumi varajasest noorusest ehkki kosmoloogilised vaatlused ei suuda veel määrata Universumi praegust ulatust ega ennustada tulevikku. Universumi horisondi olemasoluga on seotud üks tänapäeva kosmoloogia põhiprobleemidest - miks on Universum homogeenne ja isotroopne? Probleemi olemust selgitab joonis 8.
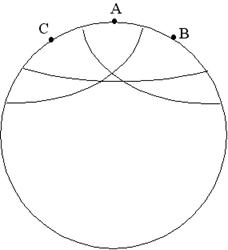
Joonis 8. Homogeensuse paradoks.
Punktis 
(kosmoloogilises
mõttes) oleva vaatleja jaoks on punktid C ja B horisondi sees. Vaatleja näeb,
et C ja B füüsikalised omadused on ühesugused. Kuidas on see võimalik? Punkt
C on ju väljapool B horisonti ning järelikult ei ole nad kunagi signaale (informatsiooni)
vahetanud.
Kuidas sai kujuneda homogeenne ja isotroopne Universum, mida kinnitavad vaatlused, kui vaadeldavas Universumi osas on palju piirkondi, mis ei ole kunagi olnud omavahel põhjuslikult seotud?
Probleemi üheks lahenduse variandiks on nn inflatsioonilised mudelid, kus eeldatakse, et väga varajases Universumis toimus Universumi paisumine palju kiiremini, kui horisondi paisumine. Sellisel juhul võivad hilisemas Friedman´i mudeli staadiumis olla kõik praegu vaadeldavad objektid pärit ühest Universumi inflatsioonilises staadiumis horisondi sisse jäävast piirkonnast. Kuigi inflatsioonilised mudelid on tänapäeval väga populaarsed, puudub siiski ühtne seisukoht inflatsioonilise paisumise staadiumi tekkepõhjuste osas.
Lõpetuseks võib öelda, et tänu horisondile on vaatleja seisukohalt erinevus kinnise ja lahtise Universumi vahel palju väiksem, kui esmapilgul näib. Mõlemal juhul on ruumi piirkond, mille kohta on võimalik informatsiooni saada, lõplik. Selle piirkonna geomeetriline struktuur vastab kinnise ruumi (positiivse kõverusega) ruumi geomeetriale - ruumala on lõplik, äärepinna pindala võrdub nulliga.