§1. KORRAPÄRASTE HULKTAHUKATE JOONESTAMINE
Korrapärased hulktahukad on tetraeeder, kuup, oktaeeder, ikosaeeder
ja dodekaeeder. Korrapäraste hulktahukate ja mõnede neist tuletatud
kehade joonestamiseks pakub lihtsaid võimalusi Mathematica
programmifail Graphics`Polyhedra`. Täiuslikumaid programme
mitmesuguste hulktahukate joonestamiseks võib leida Interneti aadressidel
[14] ja [15].
Loeme faili Graphics`Polyhedra` mälusse.
In[1]:=
<<Graphics`Polyhedra`
Näide 1. Korraldus Polyhedra väljastab loetelu
packages
defineeritud hulktahukatest.
In[2]:=
Polyhedra
Out[2]=
{Tetrahedron, Cube, Octahedron, Dodecahedron,
Icosahedron, Hexahedron, GreatDodecahedron,
SmallStellatedDodecahedron,
GreatStellatedDodecahedron, GreatIcosahedron}
Loetelust ilmneb, et lisaks platoonilistele kehadele on spetsiaalsed
väljendid veel mõnede kehade tähistamiseks.
Hulktahukatega töötamiseks on programmifailis defineeritud
rida spetsiaalseid korraldusi, millest huvitavamaid järgnevalt vaatame.
Polyhedron[tahukas] Siin tahukas
on üks eelmises loendis toodud kehadest. Korraldus Polyhedron
genereerib
vastava kolmemõõtmelise graafika objekti. Objekti saab ekraanile
tuua Show abil.
Näide 2. Joonestame oktaeedri.
In[3]:=
Show[ Polyhedron[ Octahedron ]]
OpenTruncate[Polyhedron[tahukas]]
Lõikab
ära hulktahuka tipud.
OpenTruncate[Polyhedron[tahukas],
k]
Siin
arv k Î
[0; 0.5[
näitab, kui suur osa tipust ära lõigatakse.
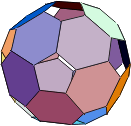
Näide 3. Joonestame lõigatud tippudega dodekaeedri.
Parameetriga Boxed->False jätame kasti joonise ümbert
ära.
In[4]:=
Show[ OpenTruncate[
Polyhedron[ Icosahedron ]],
Boxed->False]
Truncate[Polyhedron[tahukas]] Lõikab
samuti ära hulktahuka tipud. Erinevalt eelmisest käsust kleebitakse
lõikekohad kinni, nii et tekib mulje massiivsest kehast. Lõike
ulatust saab määrata analoogiliselt käsuga OpenTruncate.
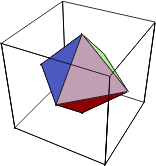
Näide 4. Joonestame oktaeedri, mille tipud lõikame
ära 0,34 osa ulatuses serva pikkusest.
Käsu Polyhedron poolt koostadud kolmemõõtmelise
graafika objekt koosneb Polygon-tüüpi graafika primitiividest,
antud juhul viisnurkadest ja kuusnurkadest. Värvime viisnurgad siniseks,
kuusnurgad aga jätame valgeks. Selleks kontrollime, kas Polygoni
argument sobib malliga x_/;Length[x]==5. Kui sobib, asendame
Polygoni loendiga {RGBColor[0,0,1], Polygon[x]}. Parameetriga
Background muudame tagapõhja värvi ja parameetriga
LightSources valgustust.
In[5]:=
Show[ Truncate[
Polyhedron[ Icosahedron ], 0.34 ]/.
Polygon[x_/;Length[x]==5]->
{SurfaceColor[ RGBColor[0,0,1]], Polygon[x] },
LightSources
-> {{{0.7,1,1.2},GrayLevel[1]},
{{0.5,-1,1}, GrayLevel[0.3]}},
Boxed
-> False,
Background
-> RGBColor[0.04, 0.79, 0.17] ]

Stellate[Polyhedron[tahukas], k]
Ehitab
keha igale tahule püramiidi. Mittekohustuslik arv k näitab
püramiidi kõrgust. Kui k > 1, siis jääb püramiidi
tipp hulktahuka pinnast kõrgemale, seega saame kumera keha. Kui
k
< 1, jääb tahk nõgusaks.
Näide 5. Ehatäht.
In[6]:=
Show[ Stellate[
Polyhedron[ Dodecahedron ],4],
Boxed
-> False,
LightSources
-> {{{1,0.7,1},RGBColor[1,0.89,0.01]},
{{-1,-1,1},RGBColor[0.72,0.52,0.043]}},
Background
-> RGBColor[0.098, 0.098, 0.44] ]

§2. ITERATSIOONIMEETODITEST
Iteratsioonimeetodiks nimetatakse teatud võtet võrrandite,
võrrandisüsteemide, ekstreemumülesannete jms. ligikaudseks
lahendamiseks. Kõigi iteratsioonimeetodite põhiidee seisneb
järgnevas: ülesandele leitakse mingi alglähend x1
,
mille abil moodustatakse lähendite jada
x1 ; x2 ; x3 ;
; xn ;
.
Teatud tingimustel koondub see jada ülesande täpseks lahendiks
x*.
Pikemalt on iteratsioonimeetoditest juttu raamatus [11].
Allpool vaatleme võrrandite lahendamist hariliku iteratsioonimeetodi
ja Newtoni meetodi abil. Sellel käsitlusel on põhiliselt illustratiivne
väärtus, sest praktiliselt on mugavam võrrand lahendada
näiteks käsuga FindRoot. Ka FindRoot leiab
lahendi iteratsioonimeetodiga, kuid sel juhul ei ole võimalik jälgida
lähendite jada koostamist.
2.1. Harilik iteratsioonimeetod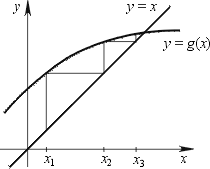
Kokkuvõte teooriast Olgu meil antud võrrand kujul
g(x)
= x. Alglähendite jada moodustatakse järgmise eeskirjaga
abil:
xn+1 = g(xn).
Jada x1; x2; x3;
; xn;
koondub võrrandi täpseks lahendiks
x*,
kui mingis jada elemente ja võrrandi täpset lahendit sisaldavas
vahemikus on täidetud tingimus
| g'(x) | £
q
< 1. (1)
Näide 1. Lahendame võrrandi e x/4
+
x 8 = 0. Hariliku iteratsioonimeetodi rakendamiseks tuleb teisendada
võrrand kujule g(x) = x. Seda on võimalik
teha mitmel eri viisil, kusjuures sellest, kuidas on valitud funktsioon
g(x),
sõltub lahendite jada koondumise kiirus. Üks võimalus
oleks näiteks 8 e x/4 = x.
Seega nüüd g(x) = 8 e x/4
. Kuna seda funktsiooni on vaja korduvalt kasutada, defineerime ta. Et
edaspidi saaksime g(x) väärtused kümnendmurruna,
kasutame defineerimisel funktsiooni N.
In[1]:=
g[x_] := N[ 8-E^(x/4)]
Kas funktsioon g(x) rahuldab tingimust (1)? Eksponentfunktsiooni
omadusi teades on kerge näha, et tingimus (1) on täidetud mingis
lõpmatus vahemikus. Valime alglähendiks näiteks x1
= 8 ja arvutame vastavalt iteratsioonieeskirjale järgmised lähendid:
In[2]:=
x1=8; x2=g[x1]
Out[2]=
0.610944
In[3]:=
x3=g[x2]
Out[3]=
6.83498
In[4]:=
x4=g[x3]
Out[4]=
2.47797
Programminäide Neid arvutusi oleks ratsionaalne teha mingi
tsükli, näiteks While-tsükli abil. While-lause
süntaks on järgmine.
While[tingimus, laused]
Esmalt
arvutatakse
tingimuse väärtus ja siis täidetakse
laused.
Tegevust korratakse seni, kuni tingimus püsib tõesena.
Märkus. Praegu vaatan, et siin oleks hoopis elegantsem
kasutada FixedPointList'i, aga kuidagi pole aega kseda kohta ümber
teha. Jäägu see lugejale iseseisvaks programmeerimisharjutuseks.
Esitame programmilõigu, mis arvutab xi-sid
seni, kuni avaldis | g(xi) xi
| > 0,001. Juhuks, kui iteratsiooniprotsess hajub, on lisatud tingimused,
mis lõpetavad programmi töö, kui xi
satub väljapoole piirkonda [xmin ; xmax].
Käsuga AppendTo kirjutatakse iga leitud lähend xi
ja temale vastav g(xi) väärtus loendisse
lahendid.
Võtame xmin = 10 ; xmax
= 10 ja alglähend x1 = 8.
In[5]:=
xi = 8;
xmin
= -10; xmax = 10;
lahendid
= {{xi,g[xi]}};
While[
Abs[g[xi]-xi]>0.001 && xi>xmin && xi<xmax,
xi = g[xi];
AppendTo[ lahendid, {xi,g[xi]} ]
]
Väljastame lähendite xi-de loendi lahendid
ekraanile. Et saada tulemust tabeli kujul, kasutame korraldust TableForm.
Parameetriga TableHeadings lisame tabelile päise ja nummerdame
read.
In[6]:=
TableForm[ lahendid,
TableHeadings -> {Automatic,{"xi","g(xi)"}}]
Out[6]//TableForm=
xi g(xi)
1 8 0.610944
2 0.610944 6.83498
3 6.83498 2.47797
4 2.47797 6.14202
.
. . . . . . . . . . . . . . . . . . . . . .
42 4.73329 4.7348
43 4.7348 4.73357
44 4.73357 4.73457
45 4.73457 4.73375
Seega võrrandi ligkaudne lahend on x »
4,73 ja selleni jõudmiseks läks vaja 45 iteratsioonisammu.
Iteratsioonisammude suur arv on tingitud sellest, et harilik iteratsioonimeetod
koondub aeglaselt, aga ka sellest, et valisime suhteliselt halva alglähendi.
Kui me ei soovi ekraanile kuvada tervet lähendite jada, siis võib
küsida korraldusega Last loendi lahendid viimase elemndi
väärtust.
In[7]:=
Last[ lahendid]
Out[7]=
{4.73457, 4.73375}
Iteratsioonide arvu saame teada, küsides loendi lahendid elementide
arvu, sest igal sammul kirjutati loendisse üks element.
In[8]:=
Length[lahendid]
Out[8]=
45
Kontrolliks leiame võrrandi 8 e x/4
=
x lahendi käsuga FindRoot.
In[9]:=
FindRoot[g[x]==x, {x,8}]
Out[9]=
{x -> 4.73412}
Graafiline interpretatsioon Geomeetriliselt tähendab võrrandi
g(x)
= x lahendamine joonte y = g(x) ja y
= x lõikepunkti x-koordinaadi leidmist. Teeme joonise,
x-telje
piirkonna võtame näiteks [ 2; 10].
In[10]:=
Plot[{g[x],x}, {x,-2,10},
AspectRatio->Automatic,
PlotStyle->RGBColor[0,0,1]]
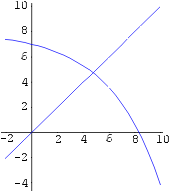
Lähendite jada koondumise protsessi võib kujutada graafiliselt,
vt. joonist teooriakokkuvõtte juures. Seame eesmärgiks koostada
analoogiline joonis ka meie näite jaoks. Joonte y = 8 e
x / 4 ja y = x graafikud on ülalpool juba
olemas. Neile oleks vaja lisada lähendite jada koondumist näitav
murdjoon.
Murdjoon algab punktist (x1; x1)
ja seejärel läbib punkte (x1; g(x1))
; (x2; x2) ; (x2;
g(x2))
jne. Konstrueerime kõigepealt sellise punktide jada. Nõutud
jada saaksime loendist lahendid, kui lisada seal iga punkti (xi;
yi)
ette punkt (xi; xi). Teisisõnu,
tuleb asendada punkt (xi; yi) punktipaariga
( (xi;
xi) ; (xi;
yi)
).
Seda saab teha järgimise asendamiskäsuga:
In[11]:=
pts = lahendid /. {x_,y_} -> {{x,x},{x,y}};
Saadud loendis pts on punktid kahekaupa alamloenditesse grupeeritud.
Ülearused alamloendid saab eemeldada käsuga Flatten.
In[12]:=
pts = Flatten[pts,1];
Rakendame punktide loendile graafikaprimitiivi Line.
In[13]:=
j = Line[pts];
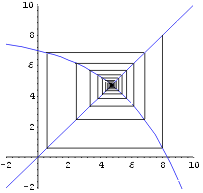
Ning lõpuks esitame ühel joonisel funktsioonide graafikud
ja murdjoone j. Parameetriga PlotRange täpsustame joonise piirkonda.
In[14]:=
Show[ %10, Graphics[j],
PlotRange->{{-2,10},{-2,10}}]
2.2. Newtoni meetod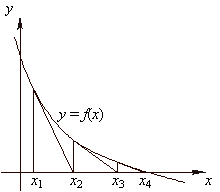
Kokkuvõte teooriast Olgu meil antud võrrand kujul
f(x)
= 0.
Valime alglähendi x1 ja koostame lähendite
jada järgmise eeskirja abil:
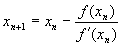
Newtoni meetodi korral saame lähendite jada järgmise liikme
xi+1,
kui leiame punktis xi graafikule tõmmatud puutuja
lõikepunkti x-teljega. Seda mõttekäiku selgitab
allolev joonis.
Näide 2. Lahendame võrrandi 3 x 4
2 x + 0,4 = 0.
Newtoni meetodi korral on järgmise lähendi xn+1
arvutamiseks vaja ka funktsiooni f(x) tuletise väärtust
kohal xn. Selleks defineerime koos funktsiooniga f(x)
ka tema tuletisfunktsiooni f'(x).
In[15]:=
f[x_] := N[ 3^(x-4) - 2^x + 0.4];
Df[x_] = D[f[x],x]
Out[15]=
x -4.
+ x
-0.693147 2. + 1.09861 3.
Väljundreal on funktsiooni tuletis f'(x). (Logaritmid
on välja arvutatud.)
Tuletisfunktsiooni defineerimisel ei tohi kasutada viivitusega omistamist,
mida funktsioonide defineerimisel harilikult kasutatakse. Viivitusega omistamise
korral oodataks tuletise võtmisega nii kaua, kuni sisestatakse rida
Df[xi], s.t., on vaja arvutada Df väärtus kohal
xi. Sel juhul jõuab programm olukorrani, kus diferentseerida
tuleb xi järgi, mis on võimatu, sest xi on
arv.
Lähendid arvutame tsükli abil, mis on analoogiline hariliku
iteratsioonimeetodi jaoks toodule, erinevus on vaid xi
arvutamises.
In[16]:=
xi = 2.5;
xmin = -10; xmax = 10;
lahendid = {{xi,f[xi]}};
While[
Abs[f[xi]]>0.0001 && xi>xmin && xi<xmax,
xi = xi - f[xi]/Df[xi];
AppendTo[lahendid, {xi,f[xi]} ]
]
In[17]:=
TableForm[ lahendid,
TableHeadings -> {Automatic,{"xi","f(xi)"}} ]
Out[17]//TableForm=
xi f(xi)
1 2.5 -5.0644
2 1.13479 -1.75291
3 -0.0537329 -0.551802
4 -0.896153 -0.132705
5 -1.25738 -0.0152012
6 -1.31043 -0.000274214
-8
7 -1.31142 -9.36672 10
Seitsme iteratsioonisammuga jõudsime lahendini x »
1,31.
Vaatame, millise lahendi annab võrrandile FindRoot.
In[18]:=
FindRoot[f[x]==0, {x,2.5}]
Out[18]=
{x -> -1.31142}
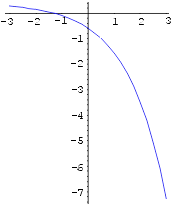
Graafiline interpretatsioon Võrrandi f(x)
= 0 lahendamine tähendab graafiliselt joone y = f(x)
ja x-telje lõikepunkti abstsissi leidmist. Joonestame funktsiooni
f(x)
= 3 x 4 2 x + 0,4 graafiku. Joonise
x-telje
piirkond olgu näiteks [ 3; 3 ].
In[19]:=
Plot[f[x], {x,-3,3},
AspectRatio -> Automatic,
PlotStyle -> RGBColor[0,0,1]]
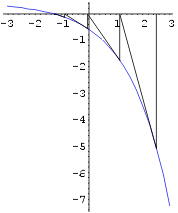
Kuidas lähendite jada koondumist graafiliselt illustreerida on
näha Newtoni meetodi kirjelduses toodud joonisel, vt. eespoolt. Iga
lähendi korral on tõmmatud ristlõik x-teljelt
graafikuni ja graafikult on võetud puutuja x-teljeni. Puutuja
ja x-telje lõikepunktis on järgmine lähend. Neid
lõike võib vaadelda murdjoonena, mis algab punktist (x1;
0) ja edasi läbib punkte (x1 ; f(x1))
; (x2 ; 0); (x2 ; f(x2))
jne. Sellise punktide loendi saame, kui loendis lahendid iga punkti (xi
;
yi
)
asendame punktipaariga ( (xi
; 0) ; (xi
;
yi
)
).
In[20]:=
pts = lahendid /. {x_,y_} -> {{x,0},{x,y}};
j = Line[ Flatten[pts,1] ];
In[21]:=
Show[ %19, Graphics[j]]
§3. TEIST
JÄRKU JOONE ÜLDVÕRRANDI LIHTSUSTAMINE
Teist järku jooneks nimetatakse joont, mille võrrandis võivad
esineda liikmed muutuva punkti X koordinaatide x ja y
esimese ja teise astmega või nende muutujate korrutisega ning vabaliikmed.
Teist järku joone võrrandi üldkuju on:
a11x2
+ 2a12xy + a22y2
+ 2a10x + 2a20y + a00
= 0,
kus a11 , a12 , a22
, a10 , a20 ja a00
on konstantsed kordajad. Sõltuvalt kordajate väärtusest
võib teist järku joon olla ellips, parabool, hüperbool
või mõni nende joonte kidunud alajuhtum. Kuna nimetatud jooned
tekivad koonuse ja tasandi lõikumisel, siis nimetatakse teist järku
jooni ka koonuslõigeteks. Lisamaterjali teist järku joonte
kohta võib leida raamatutest [7] ja [8].
3.1. Joone tüübi määramine
Kokkuvõte teooriast Et teha kindlaks, millist joont esitab
konkreetne võrrand, tuleb arvutada teatavad suurused, mida nimetatakse
invariantideks. Teist järku joone invariandid on:
S = a11
+ a22
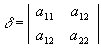
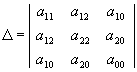
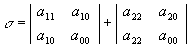
Allpool olev tabel selgitab, kuidas invariantide järgi joone tüüpi
määrata. Koos iga joone nimetusega on toodud ka joone kanooniline
võrrand, s. o. joone võrrand kanoonilise reeperi suhtes.
|
D ¹
0
|
D = 0
|
|
d < 0
|
Hüperbool
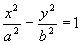
|
Kaheks lõikuvaks sirgeks kidunud hüperbool
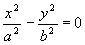
|
|
d = 0
|
Parabool
y2 = 2px
|
s < 0
|
Kaks reaalset parallelset sirget
y2 = a2
|
s = 0
|
Üks kahekordne sirge
y2 = 0
|
|
s > 0
|
Kaks imaginaarset paralleelset sirget
y2 = a2
|
|
d > 0
|
SD < 0
|
Ellips
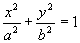
|
Punktiks kidunud ellips
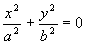
|
|
SD > 0
|
Imaginaarne ellips 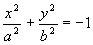
|
Näide 1. Olgu antud teist järku joon võrrandiga
5x2 + 4xy + 8y2 32x
56y + 80 = 0.
Koostame programmi, mis abistaks kasutajat joone tüübi määramisel.
Tekib küsimus: millisel kujul peaksid olema selle programmi sisendandmed?
Kas kasutaja sisestab joone üldvõrrandi või ainult kordajad
a11,
a12,
?
Sageli on joone võrrand saadud teisenduste tulemusena. Kordajate
avaldised võivad olla vägagi keerukad; sel juhul on mugavam
kasutada olemasolevat võrrandit, mitte hakata kordajaid klaviatuurilt
sisestama. Sellest kaalutlusest lähtudes tasub võrrandist kordajate
a11,
a12,
leidmiseks koostada omaette funktsioon.
Kordajate leidmine Kirjutame funktsiooni, mis teist järku
joone võrrandi sisestamisel väljastaks kordajad a11,
a12,
.Võrrandi vasak pool on kahe muutujaga polünoom, mille tähistame
P-ga.
In[1]:=
P = 5x^2 + 4x y + 8y^2 - 32x - 56y + 80;
Polünoomi kordajaid saab küsida käsuga Coefficient.
Coefficient[poly, x, n]
Annab
liikme
xn kordaja. Seejuures loetakse, et
poly
on ühe muutuja x polünoom. Näiteks püüdes
küsida
x-i kordajat meie polünoomis, saame:
In[2]:=
Coefficient[P, x, 1]
Out[2]=
-32 + 4 y
Muutuja x kordaja saamiseks peame tulemusele rakendama veel
kord käsku Coefficient ja nüüd seadma tingimuseks,
et y-i aste oleks 0.
In[3]:=
Coefficient[%, y, 0]
Out[3]=
-32
Seda põhimõtet kasutades leiab allpool toodud funktsioon
Kordajad arvud a11, a12,
.
In[4]:=
Kordajad[ poly_?PolynomialQ==0, {x_,y_}] :=
{Coefficient[ Coefficient[poly,x,2], y,0],
Coefficient[ Coefficient[poly,x,1], y,1]/2,
Coefficient[ Coefficient[poly,x,0], y,2],
Coefficient[ Coefficient[poly,x,1], y,0]/2,
Coefficient[ Coefficient[poly,x,0], y,1]/2,
Coefficient[ Coefficient[poly,x,0], y,0]}
(* Annab kordajad loendina sellises järjekorras:
{a11,a12,a22,a10,a20,a00} *)
Funktsiooni argumentideks on joone võrrand ja võrrandi
muutujate kaheelemendiline loend. Muutujate määramine on oluline,
sest siis saab töötada ka selliste võrranditega, mis ei
sõltu
x-st ja y-st, vaid näiteks u-st
ja v-st. Joone võrrandi vasak pool peab olema polünoom.
Seda kontrollitakse malliga _?PolynomialQ. Võrrandi paremal
poolel peab olema null. Funktsioon väljastab kordajad loendina kindlas
järjekorras. Järjekord on siin väga oluline, seetõttu
on funktsioonile lisatud seda meenutav kommentaar.
In[5]:=
{a11,a12,a22,a10,a20,a00} = Kordajad[ P==0, {x,y}]
Out[5]=
{5, 2, 8, -16, -28, 80}
Seega, a11 = 5, a12 = 2 (s. o.
1/2
xy kordajast) jne.
Joone tüübi määramine Joone tüübi
määramiseks tuleb arvutada invariandid d
, D , S ja s
.
In[6]:=
delta = Det[{{a11,a12},{a12,a22}}]
Out[6]=
36
In[7]:=
Delta = Det[
{{a11,a12,a10}, {a12,a22,a20}, {a10,a20,a00}} ]
Out[7]=
-1296
Võib juhtuda, et viimase rea sisestamisel väljastatakse
teade uus muutujanimi Delta on sarnane olemasolevale nimele
delta. Sel juhul tuleks Delta arvutamise real veel kord
vajutada klahve [Shift] + [Enter], teiste sõnadega, rida uuesti
sisestada.
Oleme saanud, et d > 0 ja D
¹
0 ja ilmselt SD
< 0. Seega esitab
meie võrrand reaalset ellipsit, vt. tabelit eespool.
Programminäide Toome ära ühe võimaliku
programmi, mis sisaldab nii invariantide arvutamist kui ka joone liigi
määramise tabelit.
In[8]:= Joonetyyp[{a11_,a12_,a22_,a10_,a20_,a00_}]
:=
Module[
{
S = a11+a22,
delta = Det[{{a11,a12}, {a12,a22}}],
Delta = Det[{{a11,a12,a10}, {a12,a22,a20}, {a10,a20,a00}}],
sigma = Det[{{a11,a10}, {a10,a00}}]+
Det[{{a22,a20}, {a20,a00}}] },
Which[
Delta!=0 && delta<0, "Hyperbool",
Delta!=0 && delta==0, "Parabool",
Delta!=0 && S*Delta<0, "Ellips",
Delta!=0 && S*Delta>0, "Imaginaarne ellips",
delta<0, "Lõikuvateks sirgeteks kidunud hyperbool",
delta==0 && sigma<0, "Kaks reaalset paraleelset sirget",
delta==0 && sigma==0, "Yks kahekordne sirge",
delta==0 && sigma>0, "Kaks imaginaarset paralleelset sirget",
delta>0, "Punktiks kidunud ellips"] ]
Funktsiooni argumendiks on võrrandi kordajate loend. Invariandid
S, delta, Delta ja sigma arvutatakse
Module lokaalsete muutujatena. Joone liik määratakse tingimuslausega
Which. Meenutame Which-käsu süntaksit.
Which[tingimus1, väärtus1,
tingimus2,
väärtus2,
...]
Kui
tingimus1
on täidetud, siis annab Which-lause tulemuseks
väärtus1.
Kui tingimus1 ei ole täidetud, siis kontrollitakse tingimus2.
Kui see on täidetud, siis on tulemuseks
väärtus2
jne.
Which-lause lõpetab töö niipea, kui üks
tõene tingimus on leitud. Seetõttu pole tingimust Delta==0
vaja
joone kidunud juhtumite korral vaja lisada. Meenutame, et loogilist ja-d
märgitakse sümbolitega && ning mittevõrdumist
sümbolitega != .
Näiteülesande kordajad leidsime 5. real, seega võime
neid nüüd kasutada.
In[9]:=
Joonetyyp[%5]
Out[9]=
Ellips
Teist järku joon osutus ellipsiks, mis ühtib varem saadud
tulemusega.
Näide 2. Leiame, millist joont esitab võrrand 2x2
3xy 4y2 + 5y = 0.
In[10]:=
Joonetyyp[ Kordajad[
2x^2 - 3x y - 4y^2 + 5y == 0, {x,y} ]]
Out[10]=
Hyperbool
3.2. Joone võrrandi lihtsustamine
Kokkuvõte teooriast Olgu antud teist järku joon võrrandiga
a11x2
+ 2a12xy + a22y2
+ 2a10x + 2a20y + a00
= 0. (1)
Kuidas paikneb see joon koordinaatteljestikus? Milline on täpsemalt
joone kuju? Neile küsimustele vastamiseks võetakse kasutusele
selline koordinaatteljestik, mille suhtes joon on kanoonilises asendis,
s. t. joone keskpunkt asub reeperi alguspunktis ja joone sümmeetriateljed
on paralleelsed koordinaattelgedega. Leitakse joone võrrand selle
teljestiku suhtes. See on joone kanooniline võrrand, mille järgi
on lihtne leida tema pooltelgi, ekstsentrilisust, joont skitseerida jms.
Kui võrrandis (1) kordaja a12 ¹
0, siis joone teljed ei ole koordinaattelgedega paralleelsed, vaid on pööratud
nurga a võrra. Nurga a
saab leida võrrandist
a12 k2
+ (a11 a22) k a12
= 0, kus k = tan a .
Pöörame koordinaatteljestikku (reeperit) nurga a
võrra ja leiame joone võrrandi pööratud teljestiku
suhtes. Olgu joone suvalise punkti koordinaadid esialgse reeperi suhtes
(x; y) ja sellesama punkti koordinaadid pööratud
reeperi suhtes (x1; y1). Siis kehtivad
valemid
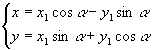 .
.
ehk maatrikskujul
( x y ) = ( x1
y1)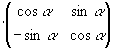 .
(2)
.
(2)
Asendades x ja y esialgsesse võrrandisse (1),
saame joone võrrandi pööratud teljestiku suhtes. Selle
võrrandi üldkuju on:
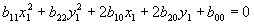 (3)
(3)
Teisenduse tulemusena peab liikme x1y1
kordaja nulliks minema.
Kui nüüd b11 ¹
0 ja b22 ¹ 0, siis joone
keskpunkti koordinaadid avalduvad valemitega
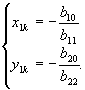
Võtame kasutusele kolmanda koordinaatteljestiku, mille teljed
on paralleelsed joone telgedega ja alguspunkt asub joone keskpunktis. Olgu
joone suvalise punkti koordinaadid kolmanda teljestiku suhtes (x2;
y2).
Sel juhul kehtivad valemid
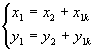
ehk maatrikskujul
( x1 y1
) = ( x2
y2 ) + ( x1k
y1k
) (4)
Asendades x1 ja y1 võrrandisse
(2), saame joone võrrandi kolmanda teljestiku suhtes. Üldkujul
on võrrand järgmine:
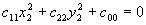 (5)
(5)
Teisenduse tulemusena peavad liikmete x2 ja y2
kordajad nulliks minema.
Viimasest võrrandist (5) on hõlpsasti välja kirjutatav
joone kanooniline võrrand.
Näide 3. Lihtsustame esimeses näites toodud joone võrrandi
5x2 + 4xy
+ 8y2 32x 56y + 80 = 0.
Reeperi pööre Eeldame, et muutujad P,
a11, a12, a22, a10, a20 ja
a00 on eelmises punktis juba defineeritud.
Leiame nurga a .
In[11]:=
Solve[a12 k^2 + (a11-a22) k-a12 == 0, k]
Out[11]=
1
{{k -> -(-)}, {k -> 2}}
2
Saime kaks lahendit. Kuna hiljem läheb mõlemaid tarvis,
tähistame esimese k1-ga ja teise k2-ga.
In[12]:=
k1=k/.%[[1]]
Out[12]=
1
-(-)
2
In[13]:=
k2 = k/.%%[[2]]
Out[13]=
2
Nurga a võib määrata ükskõik
kumma k väärtuse abil.
In[14]:=
alfa = ArcTan[k2]
Out[14]=
ArcTan[2]
Leiame reeperi pöördele vastava teisenduse maatriksi M
= 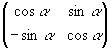 .
.
In[15]:=
M = {{ Cos[alfa], Sin[alfa]}, {-Sin[alfa], Cos[alfa]}}
Out[15]=
1 2
-2 1
{{-------, -------}, {-------, -------}}
Sqrt[5] Sqrt[5] Sqrt[5] Sqrt[5]
Avaldame x ja y koordinaatide x1 ja
y1
kaudu, kasutades valemeid (2).
In[16]:=
{x,y} = Simplify[ {x1,y1}.M ]
Out[16]=
x1 - 2 y1 2 x1 + y1
{---------, ---------}
Sqrt[5] Sqrt[5]
Kui nüüd küsida polünoomi P väärtust,
siis Mathematica asendab seal x ja y nende muutujate
väärtuseks olevate avaldistega. Lihtsustame tulemuse ja tähistame
ta P1-ga.
In[17]:=
P1=Simplify[P]
Out[17]=
144 x1 2 8 y1
2
80 - ------- + 9 x1 + ------- + 4 y1
Sqrt[5] Sqrt[5]
Pööratud koordinaatteljestiku suhtes vaadeldava joone võrrand
on
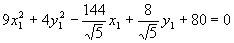 .
.
Reeperi lüke Leiame viimasest võrrandist kordajad,
tähistame neid b11, b12,
.
In[18]:=
{b11,b12,b22,b10,b20,b00} = Kordajad[P1==0, {x1,y1}]
Out[18]=
-72 4
{9, 0, 4, -------, -------, 80}
Sqrt[5] Sqrt[5]
Arvutame joone keskpunkti koordinaadid.
In[19]:=
{x1k,y1k} = {-b10/b11, y1k=-b20/b22}
Out[19]=
8 1
{-------, -(-------)}
Sqrt[5] Sqrt[5]
Märkus: Need on joone keskpunkti koordinaadid pööratud
reeperi suhtes. Et saada keskpunkti koordinaate (xk ;
yk)
esialgse reeperi suhtes, tuleb punktile (x1k
;
y1k)
rakendada pöörde valemeid.
In[20]:=
{xk,yk} = {x1k,y1k}.M
Out[20]=
{2, 3}
Leiame joone võrrandi kolmanda koordinaatteljestiku suhtes.
Avaldame
x1 ja y1 koordinaatide x2
ja y2 kaudu, kasutades valemeid (4).
In[21]:=
{x1,y1} = {x2,y2}+{x1k,y1k}
Out[21]=
8
1
{------- + x2, -(-------) + y2}
Sqrt[5] Sqrt[5]
Lihtsustame polünoomi P1 ja tähistame ta
P2-ga.
In[22]:=
P2 = Simplify[P1]
Out[22]=
2 2
-36 + 9 x2 + 4 y2
Saime, et joone võrrand pööratud ja nihutatud teljestiku
suhtes on
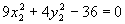 .([
)
.([
)
3.3. Teist järku joone joonestamine
Näide 4. Joonestame näites 3 vaadeldud ellipsi, mille
võrrand oli
5x2 + 4xy
+ 8y2 32x 56y + 80 = 0.
Seejuures kasutame eelmises punktis saadud tulemusi.
Võrrandist ([ ) on näha,
et ellipsi poolteljed a = 2 ja b = 3. Kui võrrandi
([ ) kordjad on keerukamad avaldised,
siis võib poolteljed a ja b leida nii:
In[23]:=
{c11,c12,c22,c10,c20,c00} = Kordajad[P2==0,{x2,y2}]
Out[23]=
{9, 0, 4, 0, 0, -36}
In[24]:=
a = Sqrt[-c00/c11]
Out[24]=
2
In[25]:=
b = Sqrt[-c00/c22]
Out[25]=
3
Ellipsi parameetrilised võrrandid pööratud koordinaatteljestiku
suhtes on
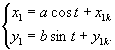
Ellipsi parameetrilised võrrandid esialgse koordinaateljestiku
suhtes saame, kui korrutame neid võrrandeid teisenduse maatriksiga
M.
In[26]:=
{X,Y} = Simplify[
{a Cos[t]+x1k, b Sin[t]+y1k}.M]
Out[26]=
2 Cos[t] 6 Sin[t] 4 Cos[t]
3 Sin[t]
{2 + -------- - --------, 3 + -------- + --------}
Sqrt[5] Sqrt[5]
Sqrt[5] Sqrt[5]
Joonestame ellipsi.
In[27]:=
ellips = ParametricPlot[{X,Y}, {t,0,2 Pi},
AspectRatio->Automatic]
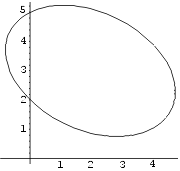
Joonestame ka võrrandi lihtsustamisel abiks olnud koordinaatteljestikud.
Pööratud reeperi telgedeks sobivad kaks sirget, mille tõusud
k1
ja k2 ning mis läbivad punkti (0; 0). Arvestame,
et nende sirgete võrrandid esituvad kujul y = kx ja
joonestame nad piirkonnas [ 2; 6] sinise joonega.
In[28]:=
reeper1 = Plot[ {k1 x, k2 x}, {x,-2,6},
DisplayFunction -> Identity,
PlotStyle -> RGBColor[0,0,1] ];
Pööratud ja nihutatud reeperi telgedeks sobivad sirged, mille
tõusud on samuti k1 ja k2, kuid
mis läbivad punkti (xk ; yk).
Arvestame, et nende sirgete võrrandid esituvad kujul y =
yk
+ k (x xk) ja joonestame nad samas piirkonnas
punase joonega.
In[29]:=
reeper2 = Plot[ {yk+k1(x-xk), yk+k2(x-xk)}, {x,-2,6},
DisplayFunction -> Identity,
PlotStyle -> RGBColor[1,0,0] ];
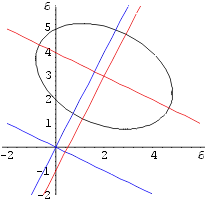
Esitame ellipsi ja koordinaatteljed ühel joonisel.
In[30]:=
Show[ ellips, reeper1, reeper2,
PlotRange -> {-2,6},
DisplayFunction -> $DisplayFunction]
§4. NÄITEID
DIFERENTSIAALGEOMEETIRAST
Selles paragrahvis vaadeldakse kahte diferentsiaalgeomeetria teemat. Neist
esimene on joone kõveruse ja väände arvutamine ning teine
evoluudi võrrandite leidmine ja evoluudi joonestamine. Nende küsimuste
põhjalik teoreetiline käsitlus on toodud raamatus [9]. Huvitavaid
diferentsiaalgeomeetria ja üldse geomeetria alaseid
Mathematica
faile võib leida Interneti aadressilt [13].
4.1. Joone kõverus ja vääne
Kokkuvõte teooriast Vaatleme ruumijoont, mis on antud parameetrilise
vektorvõrrandiga
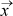 = ( x(t)
; y(t) ; z(t) ), kus t Î
[t1 ; t2].
= ( x(t)
; y(t) ; z(t) ), kus t Î
[t1 ; t2].
Võtame joonel punkti X0, millele vastab parameetri
väärtus t0 ja leiame selles punktis joonele
puutuja. Valime joonel ka teise punkti X, millele vastab parameetri
väärtus t ja milles samuti leiame joonele puutuja. Olgu
puutujate vaheline nurk j .
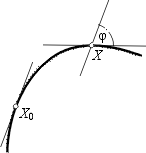
Joone kõveruseks punktis X0 nimetatakse
nurga j ja punktide X ja X0
vahlise kaare pikkuse suhte piirväärtust punkti X lähenemisel
punktile X0 mööda joont. Kõveruse tähis
on k.
Kõverus näitab, kui palju joon erineb sirgest. Kui joone
vektorvõrrand on teada, siis saab kõverust arvutada valemiga
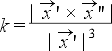 (1)
(1)
Leiame joonele punktides X ja X0 kooldumistasandid.
Olgu kooldumistasandite vaheline nurk y .
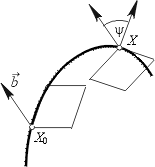
Joone väändeks punktis X0 nimetatakse
nurga y ja punktide X ja X0
vahelise kaare pikkuse suhte piirväärtust punkti X lähenemisel
punktile X0 mööda joont.
Väänet tähistatakse sümboliga  .
.
Vääne näitab, kui palju joon erineb tasandist. Kui joone
vektorvõrrand on teada, siis saab väänet arvutada valemiga
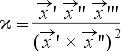 (2)
(2)
Allpool vaatame, kuidas Mathematica abil arvutada joone kõverust
ja väänet.
Näide 1. Olgu antud joon vektorvõrrandiga 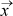 = (t cos t ; t sin t ; t) . Leiame avaldised
selle joone kõveruse ja väände arvutamiseks joone suvalises
punktis ja punktis, kus t = 8.
= (t cos t ; t sin t ; t) . Leiame avaldised
selle joone kõveruse ja väände arvutamiseks joone suvalises
punktis ja punktis, kus t = 8.
Tähistame suure X-ga vektorfunktsiooni , väikeste
tähtedega x, y ja z aga koordinaatfunktsioonid.
Seejuures kasutame kahekordset omistamist.
In[1]:=
X = {x,y,z} = {t Cos[t], t Sin[t], t}
Out[1]=
{t Cos[t], t Sin[t], t}
Põhimõtteliselt oleks siin võinud defineerimisel
näidata, et X, x, y ja z on muutuja
t funktsioonid. Sel juhul oleks sisendrida olnud X[t_] = {x[t_],y[t_],z[t_]}
= {t Cos[t], t Sin[t], t}. Antud ülesande korral on aga esimene
variant mugavam.
Suuruste k ja  arvutamise
valemites (1) ja (2) on kolm tehet, mida Mathematica põhifunktsioonide
hulgas ei ole. Need on vektorkorrutis, segakorrutis ja vektori pikkuse
arvutamine.
arvutamise
valemites (1) ja (2) on kolm tehet, mida Mathematica põhifunktsioonide
hulgas ei ole. Need on vektorkorrutis, segakorrutis ja vektori pikkuse
arvutamine.
Vektorkorrutist saab arvutada näiteks funktsiooni Cross abil,
mis on toodud § 4.3. See funktsioon on olemas ka programmifailis
LinearAlgebra`CrossProduct`. Selle faili saab mälusse lugeda
käsuga
In[2]:=
<<LinearAlgebra`CrossProduct`
Kolme vektori segakorrutis on arvutatav vektorkorrutise ja skalaarkorrutise
abil.
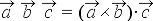
Märkus: Programmifailis Calculus`VectorAnalysis` leiduvad
muide spetsiaalsed korraldused nii vektor- kui ka segakorrutise arvutamiseks,
sellega saaks ül. lihtsamalt lahendada.
Vektori pikkus võrdub ruutjuurega tema skalaarruudust. 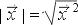 . Pikkuse arvutamiseks koostame funktsiooni d[X]. Argumendi malliga
X_?VectorQ kontrollime, et X oleks vektor.
. Pikkuse arvutamiseks koostame funktsiooni d[X]. Argumendi malliga
X_?VectorQ kontrollime, et X oleks vektor.
In[3]:=
d[X_?VectorQ] := Sqrt[X.X]
Valemi (1) järgi kirjutame funktsiooni joone kõveruse arvutamiseks.
Kõveruse avaldist on tõenäoliselt võimalik lihtsustada,
seepärast rakendame leitud avaldisele käsku Simplify.
In[4]:=
k[X_?VectorQ] := Simplify[
d[Cross[ D[X,t], D[X,t,t]]]/
d[D[X,t]]^3 ]
Funktsioon väände arvutamiseks tuleneb analoogiliselt valemist
(2).
In[5]:=
kapa[X_?VectorQ] := Simplify[
Cross[ D[X,t], D[X,t,t]].D[X,t,t,t]/
Cross[ D[X,t], D[X,t,t]].
Cross[ D[X,t], D[X,t,t]] ]
Leiame ülesandes nõutud avaldised kõveruse ja väände
jaoks joone suvalises punktis.
In[6]:=
k[X]
Out[6]=
2 4
Sqrt[8 + 5 t + t ]
-------------------
2 3/2
(2 + t )
In[7]:=
kapa[X]
Out[7]=
2
6 + t
-------------
2 4
8 + 5 t + t
Saime, et kõverus k(t) = 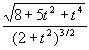 ja vääne
ja vääne  (t)
=
(t)
= 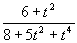 .
.
Arvutame nüüd kõveruse ja väände väärtused
punktis, kus t = 8.
In[8]:=
k[X] /. t->8
Out[8]=
553
Sqrt[---]
33
---------
33
In[9]:=
kapa[X] /. t->8
Out[9]=
5
---
316
Graafiline interpretatsioon Teame, et mida väiksem on joone
kõverus, seda sirgem on joon. Teiste sõnadega, mida väiksem
on kõverus, seda vähem erineb joon oma puutujast. Toodud näites
leidsime vektorvõrrandiga 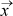 = (t cos t ; t sin t ; t) määratud
joone kõveruse punktis, kus t = 8. Joonestame võrrandiga
= (t cos t ; t sin t ; t) määratud
joone kõveruse punktis, kus t = 8. Joonestame võrrandiga 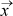 =
= 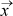 (t) määratud
ruumijoone, märgime joonel punkti P, milles parameeter t
= 8 ja joonestame talle selles punktis puutuja.
(t) määratud
ruumijoone, märgime joonel punkti P, milles parameeter t
= 8 ja joonestame talle selles punktis puutuja.
Leiame punkti P koordinaadid.
In[10]:=
P = X/.t->8
Out[10]=
{8 Cos[8], 8 Sin[8], 8}
Leiame punktis P joone puutja sihivektori 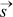 .
Puutuja sihivektori saame, kui võtame tuletise vektorfunktsioonist,
millega joon on määratud:
.
Puutuja sihivektori saame, kui võtame tuletise vektorfunktsioonist,
millega joon on määratud: 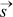 =
= 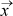 '(t).
Meid huvitab praegu puutuja punktis, kus t = 8, seega tuleb arvutada
avaldis
'(t).
Meid huvitab praegu puutuja punktis, kus t = 8, seega tuleb arvutada
avaldis 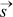 =
= 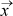 '(8).
'(8).
In[11]:=
s = D[X,t] /. t->8
Out[11]=
{Cos[8] - 8 Sin[8], 8 Cos[8] + Sin[8], 1}
Nüüd on teada puutuja sihivektor ja punkt P,
mida puutuja läbib. Joonise tegemiseks tuleb leida puutujalõigu
otspunktid. Üheks otspunktiks võtame Q1 =
P
+ l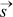 ja teiseks Q2 = P l
ja teiseks Q2 = P l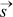 ,
kus l on mingi reaalarv. Arv l
, mis määrab puutujalõigu pikkuse, tuleb katseliselt määrata,
nii et joonis ilus tuleks. Antud ülesandes võib näiteks
võtta
l = 1,5.
,
kus l on mingi reaalarv. Arv l
, mis määrab puutujalõigu pikkuse, tuleb katseliselt määrata,
nii et joonis ilus tuleks. Antud ülesandes võib näiteks
võtta
l = 1,5.
In[12]:=
Q1 = P+1.5 s;
Q2 = P-1.5 s;
Joonestame võrrandiga 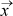 =
= 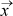 (t)
määratud ruumijoone.
(t)
määratud ruumijoone.
In[13]:=
g = ParametricPlot3D[{x,y,z}, {t,0,5 Pi},
DisplayFunction->Identity];
Funktsiooni 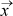 (t)
kirjutasime siin koordinaatkujul {x,y,z}. Oleks võinud
kasutada ka vektorkuju X, kuid siis ei suuda Mathematica
funktsiooni kompileerida ja väljastab vastava hoiatuse.
(t)
kirjutasime siin koordinaatkujul {x,y,z}. Oleks võinud
kasutada ka vektorkuju X, kuid siis ei suuda Mathematica
funktsiooni kompileerida ja väljastab vastava hoiatuse.
Koostame graafikaobjekti p, mis koosneb puutujast Q1Q2
ja puutepunktist P.
In[14]:=
p = Graphics3D[{
PointSize[0.04],Point[P],
Line[{Q1,Q2}]} ];
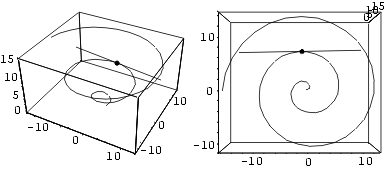
Lõpuks kanname graafiku g ja puutuja p ühele
joonisele. Parema ettekujutuse saamiseks esitame selle joonise kahes vaates.
Esimesel juhul (joonis1) kasutatame traditsioonilist vaatepunkti,
teisel juhul (joonis2) aga on vaatepunkt (0; 0; 3), s. t. objekte
vaadatakse ülalt. Korraldus GraphicsArray paigutab joonised
kõrvuti.
In[15]:=
joonis1 = Show[g, p,
DisplayFunction -> Identity];
joonis2=Show[g, p,
ViewPoint -> {0,0,3},
DisplayFunction->Identity];
Show[ GraphicsArray[ {joonis1, joonis2} ],
DisplayFunction -> $DisplayFunction]
Näide 2. Funktsioone k[X] ja kapa[X] saab
kasutada ka tasandiliste joonte korral. Leiame funktsiooni y = ln
x
kõveruse punktis x = 1.
Joone võrrandi vektorkujul on 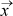 (t)
= (t, ln
t, 0). Omistame selle loendi muutujale X.
(t)
= (t, ln
t, 0). Omistame selle loendi muutujale X.
In[16]:=
X = {t,Log[x] ,0};
Arvutame joone kõveruse punktis x = 1.
In[17]:=
k[X]/.t->1
Out[17]=
1
---------
2 Sqrt[2]
Joone väände arvutamisel saame, et  º
0, sest tasandilise joone vääne on alati null.
º
0, sest tasandilise joone vääne on alati null.
In[18]:=
kapa[X]
Out[18]=
0
4.2. Joone evoluut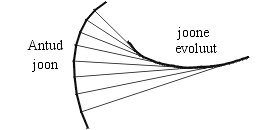
Kokkuvõte teooriast Joone evoluudiks nimetatakse
tema normaalide tasanduva parve mähisjoont. Evoluudist saab rääkida
nii ruumilise kui tasandilise joone korral. Käesolevas punktis vaatleme
tasandilise joone evoluudi leidmist Mathematica abil.
Olgu meil antud tasandiline joon parameetriliste võrranditega
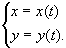 (1)
(1)
Saab tõestada, et selle joone evoluudi parameetrilised võrrandid
avalduvad kujul
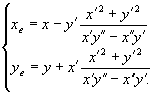 (2)
(2)
Programminäide Kui joon on antud parameetriliste võrranditega,
siis evoluudi saab leida alljärgneva funktsiooni Evoluut abil:
In[19]:=
Evoluut[{x_,y_},t_] := Module[
{p = (D[x,t]^2 + D[y,t]^2) /
(D[x,t]*D[y,t,t] - D[x,t,t]*D[y,t]) },
Simplify[{x-D[y,t]*p, y+D[x,t]*p}] ]
Funktsiooni argumentideks on joone võrrandid {x,y} ja
joone parameeter t. Viimane on vajalik, sest joone võrrandites
võib esineda rohkem kui üks muutuja ja siis on vaja teada,
milline neist on parameeter.
Evoluudi võrrandeid vaadates paneme tähele, et on kasulik
esmalt arvutada välja suurus 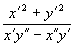 (tähistame p-ga). Evoluudi võrrandid avalduvad siis
lihtsamal kujul:
(tähistame p-ga). Evoluudi võrrandid avalduvad siis
lihtsamal kujul: 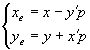 .
Suurus
p on abimuutuja, mida hiljem ilmselt tarvis ei lähe;
seepärast oleks sobiv kasutada mõnd lokaalsete muutujatega
struktuuri, näiteks Modulet. Mooduli lauseosas leitakse
evoluudi võrrandid vastavalt valemitele (2). Saadud võrrandeid
lihtsustatakse käsuga Simplify.
.
Suurus
p on abimuutuja, mida hiljem ilmselt tarvis ei lähe;
seepärast oleks sobiv kasutada mõnd lokaalsete muutujatega
struktuuri, näiteks Modulet. Mooduli lauseosas leitakse
evoluudi võrrandid vastavalt valemitele (2). Saadud võrrandeid
lihtsustatakse käsuga Simplify.
Näide 3. Leiame võrranditega 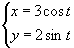 määratud ellipsi evoluudi. Et saaksime leitud võrrandeid
hiljem kasutada, omistame
määratud ellipsi evoluudi. Et saaksime leitud võrrandeid
hiljem kasutada, omistame
nad muutujatele xe ja ye.
In[20]:=
{xe,ye} = Evoluut[{3 Cos[t], 2 Sin[t]}, t]
Out[20]=
3 3
5 Cos[t] -5 Sin[t]
{---------, ----------}
3 2
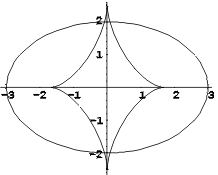
Ellipsi evoluudiks on üldistatud astroid.
Graafiline interpretatsioon Joonestame ellipsi ja tema evoluudi
graafikud.
In[21]:=
g = ParametricPlot[{{3 Cos[t], 2 Sin[t]},
{xe, ye}}, {t,0, 2 Pi},
AspectRatio -> Automatic]
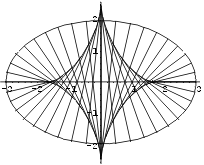
Evoluut on joone normaalide parve mähisjoon. Selle asjaolu illustreerimseks
püüame kanda joonisele ka normaalsirgete parve. Lepime kokku,
et igast normaalist joonestame välja ainult selle osa, mis jääb
joone ja evoluudi vahele.
Vaatleme ühte sellist lõiku. Lõigu alguspunkt asub
joonel punktis X0, milles joone parameeter t
omandab väärtuse t0. Lõigu lõpp-punkt
paikneb evoluudil punktis Xe0, milles evoluudi parameeter
t
omandab väärtuse t0. Seega, lõigu
alguspunkti koordinaadid on X0 ( x(t0)
; y(t0) )
ja lõpp-punkti koordinaadid Xe0(
xe(t0)
; ye(t0) ).
Koostame käsuga Table normaallõikude loendi.
In[22]:=
norm = Table[
Line[{{3 Cos[t], 2 Sin[t]}, {xe, ye}}],
{t, 0, 2 Pi, 2 Pi/40}];
Tabeli muutuja t muutub samas piirkonnas, kus joone parameeter,
see tähendab t Î [0; 2p
]. Muutuja t samm määrab normaallõikude arvu. Kui
samm on 2p /40, siis leitakse 40 normaallõiku.
Esitame ühel joonisel ellipsi, tema evoluudi ja normaalid.
In[23]:=
Show[g, Graphics[norm],
AspectRatio -> Automatic]
Programminäide Allpool on toodud programmilõik,
mis leiab joone võrrandite järgi evoluudi võrrandid,
koostab normaallõikude loendi ja väljastab ekraanile joonise.
In[24]:=
EvoluutPlot[{x_,y_}, {t_,tmin_,tmax_,n_Integer:24},opts___]:=
Module[{evol,norm},
evol = Evoluut[{x,y},t];
norm = Table[ Line[{{x,y}, evol}],
{t,tmin,tmax,(tmax-tmin)/n}];
g = ParametricPlot[{{x,y}, {evol[[1]], evol[[2]]}},
{t,tmin,tmax},
opts,
DisplayFunction -> Identity];
Show[{Graphics[norm], g},
AspectRatio -> Automatic,
DisplayFunction -> $DisplayFunction] ]
Funktsiooni argumendis muutuja n mall n_Integer:24 tähendab,
et normaalsirgete arvu märkimine ei ole funktsiooni kasutamisel kohustuslik.
Vaikimisi on normaalsirgeid 24.
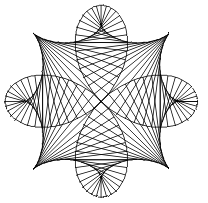
Näide 4. Joonestame funktsiooni EvoluutPlot abil
parameetrilisete võrranditega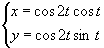 määratud
roseti evoluudi.
määratud
roseti evoluudi.
In[25]:=
EvoluutPlot[{Cos[2 t] Cos[t], Cos[2 t] Sin[t]},
{t,0,2 Pi,120}]
Eelmine
peatükk
Lisad
Sisukord










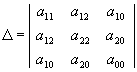
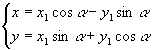 .
.
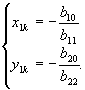
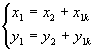
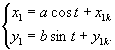




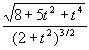 ja vääne
ja vääne 

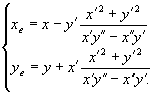 (2)
(2)
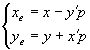 .
Suurus
p on abimuutuja, mida hiljem ilmselt tarvis ei lähe;
seepärast oleks sobiv kasutada mõnd lokaalsete muutujatega
struktuuri, näiteks Modulet. Mooduli lauseosas leitakse
evoluudi võrrandid vastavalt valemitele (2). Saadud võrrandeid
lihtsustatakse käsuga Simplify.
.
Suurus
p on abimuutuja, mida hiljem ilmselt tarvis ei lähe;
seepärast oleks sobiv kasutada mõnd lokaalsete muutujatega
struktuuri, näiteks Modulet. Mooduli lauseosas leitakse
evoluudi võrrandid vastavalt valemitele (2). Saadud võrrandeid
lihtsustatakse käsuga Simplify.


