
Kuues peatükk annab ülevaate mõndest Mathematica
programmeerimise võimalustest. Pean kurvastusega tunnistama, et
siit on välja jäänud palju olulist ja huvitavat, peamiselt
kahel põhjusel. Esiteks, kui ma seda tööd kirjutasin,
ei olnud mul sellest asjast kaugeltki mitte täielikku ülevaadet
(ja vaevalt mul seda nüüdki on) ning teiseks seadis diplomitöö
zhanr omad mahulised ja eriti ajalised piirangud.
§1. UUE FUNKTSIOONI DEFINEERIMINE
Lisaks olemasolevatele funktsioonidele võib kasutaja neid vajaduse
järgi juurde kirjutada. Funktsiooni defineerimiesel kasutatakse enamasti
niinimetatud viivitusega omistamist, mis sümbolites oleks: vp
:=
pp.
(Ehk pikemalt lahti seletatult: vasakpool
:=
parempool.)
Näide 1. Defineerime funktsiooni f(x) = x2
1.
In[1]:=
f[x_] := x^2-1
Argument kirjutatakse definitsooni vasakul poolel kandilistesse sulgudesse
ja tema järele pannakse allkriips. Allkriips tähendab, et argumendiks
võib olla suvaline avaldis. Funktsiooni f saab nüüd
kasutada nagu iga teist Mathematica funktsiooni. Küsime f
väärtust, kui x = 3.
In[2]:=
f[3]
Out[2]=
8
Arvutame f väärtuse, kui x = a.
In[3]:=
f[a]
Out[3]=
2
-1
+ a
Kui x = sin t, siis saame:
In[4]:=
f[Sin[t]]
Out[4]=
2
-1
+ Sin[t]
Joonestame f graafiku piirkonnas x Î
[ 2; 2].
In[5]:=
Plot[f[x], {x,-2,2},
AspectRatio->Automatic]

Funktsiooni f kohta saame küsida infot, nii nagu iga Mathematica
väljendi kohta. Selleks kirjutatakse väljendi ette küsimärk.
In[6]:=
?f
Out[6]=
Global`f
f[x_] := x^2 - 1
Vastuseks antakse f definitsioon.
Funktsiooni definitsiooni tühistamine Funktsiooni definitsioon
tühistatakse korraldusega Remove. Funktsiooni korral ei mõju
muutuja
väärtuse annulleerimise korraldus muutuja
=.
.
Remove[väljend] Eemaldab
mälust väljendi ja tühistab kõik talle omistatud
väärtused ja definitsioonid. Kui töö käigus tekib
vajadus funktsiooni definitsiooni muuta, funktsiooni üle defineerida,
siis on üldiselt mõistlik vana definitsioon enne Removega
tühistada, sest vastesel korral võib osa temast alles jääda
ja palju segadust põhjustada
Näide 2. Kustutame funktsiooni f.
In[7]:=
Remove[f]
Infot küsides saame nüüd:
In[8]:=
?f
Information::notfound:
Symbol f not found.
Näide 3. Kombinatsioonide arvu n elemendist k-kaupa
arvutatakse valemiga C =  . Defineerime vastava funktsiooni. Nimetusena oleks praegu mugav kasutada
C-tähte,
kuid see sümbol kuulub Mathematica võtmesõnade
hulka ja seetõttu ei saa me teda tarvitada. Teine variant oleks
näiteks Kombinatsioonid, mis on küll pikk, kuid see-eest
igale eestikeelsele kasutajale üheselt mõistetav.
. Defineerime vastava funktsiooni. Nimetusena oleks praegu mugav kasutada
C-tähte,
kuid see sümbol kuulub Mathematica võtmesõnade
hulka ja seetõttu ei saa me teda tarvitada. Teine variant oleks
näiteks Kombinatsioonid, mis on küll pikk, kuid see-eest
igale eestikeelsele kasutajale üheselt mõistetav.
In[9]:=
Kombinatsioonid[n_,k_] := n!/(k! (n-k)!)
Arvutame C53 .
In[10]:=
Kombinatsioonid[5,3]
Out[10]=
10
Näide 4. Fibonacci jada moodustavad arvud y0
= 1, y1 = 1, y2 = 2, y3
= 3, y4 = 5, y5 = 8,
. Jada kaks esimest liiget on ühed ja edasi on iga element on saadud
kahe eelmise liitmisel. Teisisõnu, jada liikmed rahuldavad rekurrentset
võrrandit
yn = yn
1 + yn 2.
Kirjutame funktsiooni, mille abil arvutatakse Fibonacci jada elemente.
Selleks kasutame rekursiivset defineerimist. Anname seose, kuidas arvutada
jada elemente eelmiste elementide kaudu, kaks esimest elementi aga defineerime
eraldi.
In[11]:=
Fibonacci[n_] := Fibonacci[n-1] + Fibonacci[n-2]
Fibonacci[0] := 1;
Fibonacci[1] := 1;
Arvutame jada 7. liikme.
In[12]:=
Fibonacci[7]
Out[12]=
21
Tavaline omistamine ja viivitusega omistamine
Tavalise omistamise sümbolkuju on vp = pp.
See on lühendatud kirjaviis käsust Set[vp,
pp].
Viivitusega omistamise sümbolkuju on vp := pp,
mis on lühend käsust SetDelayed[vp,
pp].
Tavalisel omistamisel arvutatakse parem pool välja ja hoitakse
teda alles väljaarvutatud kujul. Viivitusega omistamisel oodatakse,
kuni vasakut poolt tarvis läheb ja alles siis hakatakse arvutama parema
poole väärtust.
Näide 5. Et erinevust näha, defineerime funktsiooni
Tuletis2, mis arvutab avaldise teise tuletise muutuja t järgi.
Kasutame viivitusega omistamist.
In[13]:=
Tuletis2[x_] := D[x,t,t]
Proovime, kas meie funktsioon töötab õigesti.
In[14]:=
Tuletis2[t^4]
Out[14]=
2
12 t
Avaldise t4 teine tuletis on tõepoolest 12t2.
Defineerime tavalise omistamisega samasuguse funktsiooni Tuletis2Abi.
In[15]:=
Tuletis2Abi[x_] = D[x,t,t]
Out[15]=
0
Proovime leida funktsiooni väärtust t4
korral:
In[16]:=
Tuletis2Abi[t^4]
Out[16]=
0
Vastuseks saime 0, mis on üldjuhul vale. Põhjus on selles,
et tavalisel omistamisel arvutatakse parem pool kohe välja, s. t.
leitakse tuletis xt' . See aga on 0, sest omistamise
hetkel on x konstant. Seega on funktsiooni väärtus argumendist
sõltumata alati null. See leiab kinnitust, kui küsime funktsioonide
Tuletis2 ja Tuletis2Abi kohta infot.
In[17]:=
?Tuletis2
Out[17]=
Global`Tuletis2
Tuletis2[x_] := D[x, t, t]
In[18]:=
?Tuletis2Abi
Out[18]=
Global`Tuletis2Abi
Tuletis2Abi[x_] = 0
Enamasti kasutatakse muutujale väärtuse andmisel tavalist
omistamist, funktsiooni defineerimisel aga viivitusega omistamist, kuid
see reegel ei ole absoluutne. Vahel tuleb sisulistel kaalutlustel funktsioon
defineerida tavalise omistamisega, vt. näiteks p. 5.6.2.
§2. ARGUMENDI MALL
Eespool kirjutasime funktsiooni defineerimisel argumendi kujul x_
. Allkriips ( _ ) on argumendi mall e. pattern. Allkriips
tähendab, et funktsiooni argumendiks võib olla suvaline avaldis,
definitsiooni võib ikka kasutada. Üldiselt saab malliga seda
argumendile mitmesuguseid tingimusi ja kui tingimused ei ole täidetud,
siis definitsiooni ei kasutata.
Näide 1. Pöördume tagasi Fibonacci jada näite
juurde. Ilmselt omab selline funktsioon mõtet ainult naturaalarvulise
argumendi korral. Kui proovime arvutada näiteks Fibonacci[3.5],
väljastatakse veateated ja arvutused tuleb katkestada.
Tühistame esmalt Fibonacci vana definitsiooni. (See on vajalik!)
In[19]:=
Remove[Fibonacci]
Uuel definitsioonil kasutame argumendi malli n_Integer, s.
t. et argumendiks võib olla ainult täisarv.
In[20]:=
Fibonacci[n_Integer] :=
Fibonacci[n-1] + Fibonacci[n-2]
Fibonacci[0]:=1;
Fibonacci[1]:=1;
Küsime nüüd funktsiooni väärtust näiteks
n
= 1,2 korral.
In[21]:=
Fibonacci[1.2]
Out[21]=
Fibonacci[1.2]
Vastuseks saime sama sisendrea. Seda võiks tõlgendada
nii, et korraldusega Fibonacci ei ole seotud ühtegi definitsiooni,
mida antud juhul rakendada saaks.
Märkus. Fibonacci-funktsiooni võiks täiendada
nii, et blokeeritud oleks ka negatiivne argument.
Esitame Mathematica põhilised argumendi tüübid
koos selgituste ja näidetega.
x_Integer x on täisarv, nt. 100 , -3
x_Real x on ligikaudne arv (tunnuseks
on kümnendpunkti olemasolu), nt. 2. , 1.5289
, 5./7
x_Rational x on harilik murd, nt. 2/3 , 23^-1
x_Complex x on kompleksarv, nt. 1+I , 0.5
I
x_List x on loend, nt. {1,2}
x_Symbol x on sümbol, nt. A , õ
, £ , ±
x_String x on string, nt. "abcd"
Mõned näited argumendi malli kasutamisest:
f[x_] funktsioon f ühe suvalise argumendiga,
nt. f[1], f[x], f[Sin[x]]
f[x_,y_] funktsioon f kahe suvalise argumendiga,
nt. f[a,b], f[{4,5},99.4]
f[x_/; x>4] argument peab olema suurem kui 4, nt. f[6],
f[100.6]
f[x_g] f argumendiks on avaldis päisega g, nt.
f[g[1,2]]
f[g[x_,y_]] f argumendiks on kahe suvalise argumendiga funktsioon
g, nt. f[g[a,b]], f[g[{4,5},99.4]]
f[x__] funktsioonil võib olla üks või mitu
argumenti, nt. f[1], f[x,y]
f[x___] funktsioonil võib olla null või enam
argumenti, nt. f[], f[1], f[x,y]
f[x_?NumberQ] argument on suvaline arv, nt. f[3],
f[0.34],
f[2-3I]
f[x_?VectorQ] argument on vektor, nt. f[{a,b}], f[{0,-1,3,4}]
f[x_?MatrixQ] argument on maatriks, nt. f[{{1,2},{3,4}}]
Viimastel juhtudel on mall moodustatud funktsioonidest NumberQ[x]
ja VectorQ[x] ja MatrixQ[x].
NumberQ[x] Annab väärtuse True,
kui x on arv.
VectorQ[x] Annab väärtuse True,
kui x on vektor.
MatrixQ[x] Annab väärtuse True,
kui x on maatriks.
Analoogilisi Q-ga lõppevaid funktsioone on rohkemgi
ja mõni neist võib malli koostamisel osutuda väga kasulikuks.
Kõigi Q-ga lõppevate funktsioonide loetelu saab
ekraanile trükkida korraldusega ?*Q . Tärn *
tähistab siin suvalist arvu suvalisi sümboleid.
Seda, kas avaldis sobib mingi malliga, on lihtne kontrollida käsuga
MatchQ.
MatchQ[avaldis, mall]
Annab vastuse True, kui avaldis sobib malliga ja
False, kui ei sobi.
Näide 2.
In[22]:=
MatchQ[h[ ], h[x___]]
Out[22]=
True
See sobib.
In[23]:=
MatchQ[23, x_Real]
Out[23]=
False
Ei sobi, sest 23 ei sisalda kümnendpunkti ja seega Mathematica
käsitleb teda täisarvuna, mitte ligikaudse arvuna.
§3. ASENDAMISREEGLID
Asendamisreeglid (replacement rules) pakuvad veel ühe võimaluse
Mathematica
avaldiste teisendamiseks. Asendamisreeglite idee seisneb lühidalt
selles, et avaldises asendatakse teatud sümbolid või alamavaldised
teiste sümbolite või avaldistega. Kui näiteks tahame avaldises
a
asendada kõik b-d c-dega, siis saab seda teha
reaga a/.b->c.
Protseduuri saab vaadelda kahe osana:
b->c ehk Rule[b,
c]
on
reegel,
mis tähendab: iga sümbol b tuleb asendada sümboliga
c.
avaldis/.reegel ehk ReplaceAll[avaldis,
reegel]
See on reegli rakendamine avaldisele.
Näide 1. Asendame avaldises x2 + 4x
muutuja x muutujaga y.
In[1]:=
x^2+4x /. x -> y
Out[1]=
2
4
y + y
Arvutame saadud avaldise väärtuse, kui y = 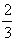 .
Selleks tuleb y asendada
.
Selleks tuleb y asendada 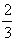 -ga.
-ga.
In[2]:=
%1 /. y -> 2/3
Out[2]=
28
--
9
Näide 2. Korraga võib avaldisele rakendada mitut
reeglit, aga sel juhul tuleb nad esitada loendina. Asendame avaldises f[x,y]
argumendi
x
z1-ga ja argumendi y z2-ga.
In[3]:=
f[x,y] /. {x->z1, y->z2}
Out[3]=
f[z1, z2]
Näide 3. Asendamisel saab kasutada malle. Olgu meil antud
mingi arvuloend.
In[4]:=
arvud = {2, -1, -2.4, 10, -3, 0, 7.2};
Asendame loendis kõik negatiivsed arvud nullidega.
In[5]:=
arvud /. x_/; x<0 -> 0
Out[5]=
{2, 0, 0, 10, 0, 0, 7.2}
Näide 4. Järgmine reegel eemaldab loendi lõpust
elemendi False.
In[6]:=
reegel = {x___,False}->{x}
Out[6]=
{x___, False} -> {x}
Siin x___ esitab loendi esimesi elemente, mida võib
olla suvaline arv. Kui loendi viimane element on False, siis mall
sobib ja loend asendatakse ainult esimestest elementidest koosneva loendiga
{x}.
In[7]:=
{a, b, False, False} /. reegel
Out[7]=
{a, b, False}
Näide 5. Vaatleme võrrandit 5x5
+ 4x3 + x + 1 = 0. Kompleksarvude vallas on sellel
võrrandil viis lahendit. Kuidas paiknevad need lahendid komplekstasandil?
(Näide on võetud raamatust [2, lk. 109].) Lahendame võrrandi
käsuga NSolve.
In[8]:=
NSolve[ 5x^5 + 4x^3 + x + 1 == 0, x]
Out[8]=
{{x -> -0.470007},
{x -> -0.185633 - 0.877206 I},
{x -> -0.185633 + 0.877206 I},
{x -> 0.420637 - 0.593597 I},
{x -> 0.420637 + 0.593597 I}}
Vastus koosneb viiest asendamisreeglist. Rakendame neid reegleid muutujale
x.
In[9]:=
x /. %8
Out[9]=
{-0.470007, -0.185633 - 0.877206 I,
-0.185633 + 0.877206 I, 0.420637 - 0.593597 I,
0.420637 + 0.593597 I}
Nüüd on võrrandi lahendid esitatud loendina. Asendame
iga reaalarvulise lahendi a arvupaariga (a; 0) ja iga kompleksarvulise
lahendi a + ib arvupaariga (a; b). Nii saadud
arvupaarid esitavad lahenditele vastavaid komplekstasandi punkte.
In[10]:=
%9 /. {a_Real->{a,0}, Complex[a_,b_]->{a,b}}
Out[10]=
{{-0.470007, 0}, {-0.185633, -0.877206},
{-0.185633, 0.877206}, {0.420637, -0.593597},
{0.420637, 0.593597}}
Teeme joonise.
In[11]:=
ListPlot[ %10,
PlotStyle->PointSize[0.05],
AspectRatio->Automatic]
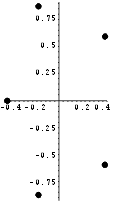
Tavaline asendamine ja viivitusega asendamine Kõigepealt
võrdluseks mõlema asendamise süntaks:
vp->pp, ehk Rule[vp,
pp]
Tavaline asendamine.
vp:>pp ehk RuleDelayed[vp,
pp]
Viivitusega asendamine.
Tavalisel asendamisel arvutatakse esmalt reegli parem pool ja siis
teostatakse asendamine. Viivitusega asendamisel toimitakse vastupidises
järjekorras.
Näide 6. Avaldise elementide arvu leitakse funktsiooni
Length[x] abil. Näiteks
In[12]:=
Length[{1,1,1}]
Out[12]=
3
In[13]:=
Length[ f[z1,z2] ]
Out[13]=
2
Märkus. Avaldise f[z1,z2] korral annab Length
argumentide
arvu, f on avaldise päis, mis ei lähe arvesse. Avaldise
{1,1,1}
päis on List. Loendi {1,1,1} asemel võiks
kirjutada List[1,1,1].
Püüame koostada reegli, mis asendaks funktsiooni f
tema argumentide arvuga.
In[14]:=
{a,b,f[z1,z2],c} /. x_f -> Length[x]
Out[14]=
{a, b, 0, c}
Tulemus on vale, sest Lengh[f[z1,z2]] on 2, mitte 0. Põhjus
on selles, et kõigepealt leiti avaldise x argumentide arv,
mis on tõepoolest 0 ja see kirjutati f[z1,z2] asemele.
Viivitusega asendamisel saame õige tulemuse.
In[15]:=
{a,b,f[z1,z2],c} /. x_f :> Length[x]
Out[15]=
{a, b, 2, c}
§4. TINGIMUSLAUSED
Sageli tekib olukordi, kus tuleb programmi tööd juhtida sõltuvalt
mingi avaldise väärtusest. Sel puhul kasutatakse tingimuslauseid.
Põhimõtteliselt taanduvad kõik tingimuslaused järgmisele
korraldusele: Kui tingimus on täidetud, tee üht; kui tingmus
ei ole täidetud, tee teist. Mathematica programmeerimiskeeles
on eri käsud nii selle kui ka mõnede keerukamate tingimuste
jaoks. Tutvustame neid lühidalt.
If[tingimus, tegevus1, tegevus2]
Kui
tingimus
on täidetud, siis tehakse tegevus1, kui tingimus ei ole täidetud,
siis tegevus2. If-lausel on kolm osa: tingimus,
tegevus1
ja tegevus2, mis peavad olema eraldatud komadega. Iga osa võib
koosneda ühest või mitmest alamlausest. Alamlaused eraldatakse
semikoolonitega. Lõpptulemuse (nn. Return-väärtuse)
määrab viimane alamlause. Tasub märkida, et võrreldes
C-keelega on siin koma ja semikooloni roll vahetatud.
Näide 1. Koostame funktsiooni, mis leiaks võrrandiga
ax2
+ bx + c = 0 määratud parabooli nullkohad ja kui
reaalsed nullkohad puuduvad, väljastaks vastava teate. Olgu funktsiooni
argumentideks võrrandi kordajad a, b ja c.
In[1]:=
NullKohad[a_,b_,c_] :=
If[ d = b^2-4 a c; d >= 0,
{(-b+Sqrt[d])/(2a), (-b-Sqrt[d])/(2a)},
"Pole reaalseid nullkohti!"]
Tingimuse osas arvutatakse kõigepealt võrrandi diskriminant
ja seejärel kontrollitakse, kas see on suurem või võrdne
nulliga. Võrrandi lahendid leitakse ruutvõrrandi lahendivalemi
abil, kuid seda võiks teha ka Solve-käsuga. Kontrollime,
kuidas funktsioon töötab.
In[2]:=
NullKohad[1,4,-12]
Out[2]=
{2, -6}
In[3]:=
NullKohad[1,2,3]
Out[3]=
Pole reaalseid nullkohti!
If[tingimus, tegevus1, tegevus2,
tegevus3]
Siin
on lisandunud tegevus3. See täidetakse siis, kui
tingimuse
tõeväärtust ei saa määrata.
Näide 2. Proovime leida avaldise NullKohad[1,m,n] väärtust.
In[4]:=
NullKohad[1,m,n]
Out[4]=
2
-m + Sqrt[d] -m - Sqrt[d]
If[d = m - 4 1 n; d >= 0, {------------, ------------},
2 1 2 1
Pole reaalseid nullkohti!]
Funktsioon ei tööta, sest ei saa määrta, kas diskriminant
on positiivne või negatiivne. Täindame funktsiooni nii, et
sellisel juhul väljastataks vastav teade.
In[5]:=
Remove[NullKohad];
NullKohad[a_,b_,c_]
:=
If[d = b^2-4 a c; d >= 0,
{ (-b+Sqrt[d])/(2a), (-b-Sqrt[d])/(2a)},
"Pole reaalseid nullkohti!",
"Kordajateks peavad olema arvud!"]
In[6]:=
NullKohad[1,m,n]
Out[6]=
Kordajateks peavad olema arvud!
Which[tingimus1, tegevus1, tingimus2,
tegevus2,
...]
Kui
tingimus1
on täidetud, siis tehakse
tegevus1 ja järgmisi tingimusi
enam ei kontrollita. Kui tingimus1 ei ole täidetud, siis kontrollitakse
tingimus2.
Kui see on annab tõese tulemuse, siis täidetakse
tegevus2
jne.
Iga tegevus võib koosneda ühest ainsast avaldisest
(siis on Which-lause tulemuseks selle avaldise väärtus)
või mitmest lausest (siis on tulemuseks viimase lause väärtus).
Üks tegevus võib kujutada ka tervet alamprogrammi. Tingimused
võivad sisaldada loogikatehteid ja võrdlustehteid (vt. §
4.6.); põhimõtteliselt võib olla tegemist väga
keeruka avaldisega.
Näide 3. Funktsioon f teeb kindlaks, kas radiaanides
antud nurk x on negatiivne nurk, teravnurk, nürinurk või
sirgnurgast suurem nurk.
In[7]:=
f[x_] := Which[
x<0, "Negatiivne nurk",
0<x<N[Pi/2], "Teravnurk",
N[Pi/2]<x<N[Pi], "Nürinurk",
N[Pi]<x, "Sirgnurgast suurem nurk" ]
Tingimustes võib kasutada korduvat võrratust, näiteks
0<x<N[Pi/2]. Konstant Pi tuleb võrdlemisel teisendada
ligikaudseks arvuks.
In[8]:=
f[2.45]
Out[8]=
Nürinurk
Switch[avaldis, väärtus1,
tegevus1,
väärtus2,
tegevus2,
]
Kui
avaldis
võrdub
väärtus1-ga, siis täidetakse
tegevus1,
kui
avaldis võrdub väärtus2-ga, siis tegevus2,
jne.
Näide 4. Funktsioon g leiab täisarvu n
kolmega jagamisel tekiva jäägi.
In[9]:=
g[n_] := Switch[ Mod[n,3],
0, "jagub", 1, "jääk 1", 2, "jääk 2"]
In[10]:=
g[652]
Out[10]=
jääk 1
Switch[avaldis, väärtus1,
tegevus1,
,
_
, tegevus(n)]
Kui avaldis ei võrdu
ühegagi väärtustest
väärtus1,
väärtus2,
, siis jõutakse võrdlemisel allkriipsuni, mis tähendab
suvalist avaldist ja täidekse tegevus(n).
Tingimuslik omistamine võimaldab anda definitsioone, mida
kasutatakse ainult teatud tingimustel. Tingimusliku omistamise üldkuju
oleks
vp:=pp/;tingimus
Seda definitsiooni kasutatakse ainult siis, kui tingimus on täidetud.
Tingimuslik omistamine võib olla ainult viivitusega omistamine.
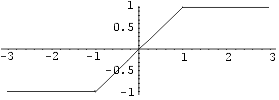
Näide 5. Vaatleme funktsiooni
h(x) = 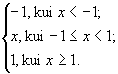
Sellise funktsiooni võib defineerida järgmiselt:
In[11]:=
h[x_]:=-1 /; x < -1;
h[x_]:=x /; -1 <= x < 1;
h[x_]:=1 /; 1 <= x;
Joonestame funktsiooni h(x) graafiku.
In[12]:=
Plot[h[x], {x,-3,3}, AspectRatio->Automatic]
§5. TSÜKLID
Kui samatüübilisi arvutusi on vaja teha palju kordi, on otstarbekas
kasutada selleks tsüklit. Tsükli korral peab olema teada, mitu
korda teda täita tuleb või peab olema mingi tingimus, mille
tõeväärtuse muutumisel tsükli töö lõpetatakse.
Mathematica
lihtsamad tsüklid on Do, While ja For.
Do-lausel on olemas järgmised süntaksivariandid:
Do[tegevus, {imax}]
Tegevust
korratakse imax korda.
Do[tegevus, {i, imax}]
Tegevust
korratakse imax korda, kusjuures muutuja
i omandab
väärtusi 1-st kuni imax-ni.
Do[tegevus, {i, imin,
imax}]
Muutuja
i
omandab väärtusi
imin-st kuni imax-ni,
sammuga 1.
Do[tegevus, {i, imin,
imax,
di}]
Muutuja
i
väärtust muudetakse sammuga di.
Do[tegevus, {i, imax},
{j,
jmax}]
Iga
i
väärtuse korral muudetakse j 1-st kuni
jmax-ni.
Näide 1. Koostame loendi Algarvud, mille elementideks
on 20 esimest algarvu.
In[1]:=
Algarvud = {};
Do[
AppendTo[ Algarvud, Prime[i] ],
{i,20}]
Selgituseks:
Prime[i] annab i-nda algarvu;
AppendTo[loend, element] lisab loendile
elemendi,
kusjuures see loend peab varem eksisteerima.
Küsime nüüd loendi Algarvud väärtust.
In[2]:=
Algarvud
Out[2]=
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71}
Märkus: Table- või Array-käsuga
oleks selle ülesande saanud lahendada lühemalt ja lihtsamalt:
Table[Prime[i],{i,20}]
või
Array[Prime,20] annavad sama tulemuse.
While[tingimus, tegevus]
Esmalt
kontrollitakse tingimust ja kui see on tõene, siis täidetakse
tegevus.
Seda korratakse seni, kuni tingimus esimest korda annab väära
tulemuse.
Näide 2. Arvu p võib
leida kui teatud rea summat:
p =  =
= 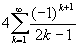 . Mitu
liiget tuleks selles summas võtta, et summa erineks tegelikust p
väärtusest vähem kui 0,01 võrra? Võtame rea
osasumma jaoks tarvitusele muutuja s algväärtusega
s=0. Loenduri k algväärtus on k=1.
. Mitu
liiget tuleks selles summas võtta, et summa erineks tegelikust p
väärtusest vähem kui 0,01 võrra? Võtame rea
osasumma jaoks tarvitusele muutuja s algväärtusega
s=0. Loenduri k algväärtus on k=1.
In[3]:=
s=0; k=1;
While[
N[Abs[Pi-s]] > 0.01,
s = s + N[4 (-1)^(k+1)/(2k-1)]; k++ ]
Väljend k++ tähendab siin sama mis k=k+1.
Küsime nüüd osasumma liikmete arvu.
In[4]:=
k
Out[4]=
101
NB! Nõutud täpsuse saavutamiseks tuleb summas võtta
tegelikult ainult 100 liiget, sest viimane kord loendurit suurendati, kuid
uut s väärtust enam ei arvutatud. Küsime, milline on summa
s
väärtus, milline p tegelik väärtus
ja kui suur on nende vahe?
In[5]:=
{s, N[Pi], N[Pi-s]}
Out[5]=
{3.13159, 3.14159, 0.00999975}
For[start, tingimus, muutus,
tegevus]
Esmalt
täidetakse lause start-osa, siis kontrollitakse, kas tingimus
on tõene ja kui on, täidetakse
muutus ja tegevus.
Kolme viimast osa korratakse, kuni ükskord
tingimus osutub
vääraks. Lause kolmas osa, muutus, sisaldab loenduri väärtuse
muutmist.
Näide 3. Korraldus FromCharacterCode[n]
annab
sümboli, mille kood on n. Trükime arvud 33 43 ja neile
vastavad sümbolid.
In[6]:=
For[ n=33, n<=43, n++,
Print[n, " ", FromCharacterCode[n]] ]
33 !
34 "
35 #
36 $
37 %
38 &
39 '
40 (
41 )
42 *
43 +
Korraldus Print[avaldis1, avaldis2,
] trükib
avaldised
ekraanile. Print-käsuga trükitud avaldised ei
moodusta väljundrida ja nende poole ei saa hiljem reanumbriga pöörduda.
Seetõttu ei peeta Print-käsu liigset kasutamist Mathematica
programmides heaks tooniks.
§6. VÕRDLUSTEHTED
JA LOOGIKATEHTED
Mõningaid võrdlustehteid kasutasime tingimuslausete ja tsüklite
koostamisel, nt. x<3, n>=0, jne. Käesolevas paragrahvis
anname Mathematica võrdlustehetest süstemaatilise ülevaate.
Esitame kõigepealt võrdlustehte sümbolkujul, seejärel
vastava võtmesõna, selgituse ja lõpuks näited.
x == y ehk Equal[x,
y]
Annab
väärtuse True, kui
x ja y on võrdsed
ja väärtuse False, kui x ja y ei ole võrdsed.
2 == 2 ---> True
2 == 3 ---> False
a == b ---> a == b Ei suuda tõeväärtust leida,
sest a ja b väärtused ei ole teada.
a1==a2==a3==
Annab väärtuse True, kui kõik ai-d
on omavahel võrdsed.
x != y ehk Unequal[x,
y]
Annab
tõese väärtuse, kui
x ¹
y.
0 != 1 ---> True
a1!=a2!=a3!=
Annab tõese väärtuse ükski ai-de
paar ei ole võrdne, st. kui iga i ¹
j
korral ai ¹
aj..
2! = 3! = 2 ---> False
x === y ehk SameQ[x,
y]
Annab
väärtuse True, kui
x ja y on identsed,
samaselt võrdsed.
a === b ---> False
Sin[ArcSin[z]] === z ---> True
x =!= y ehk UnsameQ[x,
y]
Annab
väärtuse True, kui
x ja y ei ole identsed.
a+b=!=b+a ---> False
x < y ehk Less[x,
y]
Annab
väärtuse True, kui
x < y.
2 < 3 ---> True
5 < 5.12 < 7 < 8 ---> True
5 < 5.12 < 7 < 6 ---> False
x > y ehk Greater[x,
y]
Annab
väärtuse True, kui
x > y.
x <= y ehk LessEqual[x,
y]
Annab
väärtuse True, kui
x £
y.
x >= y ehk GreaterEqual[x,
y]
Annab
väärtuse True, kui
x ³
y
Positive[x] Annab väärtuse
True, kui x > 0
Negative[x] Annab väärtuse
True, kui x < 0
NonNegative[x] Annab väärtuse
True, kui x ³ 0
Tuntumate loogikatehete jaoks on Mathematical spetsiaalsed funktsioonid.
!x ehk Not[x]
Loogiline
eitus. Hüüumärgi variandi korral esineb üks puuk, nimelt
kui ! satub rea esimeseks sümboliks, siis antakse veateade. Nii on
see käsureal töötades,
package sees vist probleemi
ei teki.
Not[2==3] ---> True
x && y &&
z
ehk And[x, y,
z,
]
Loogiline
ja. Annab tõese väärtuse, kui kõik laused x,
y,
z,
on tõesed.
Mathematica leiab järjekorras osalausete
tõeväärtused; niipea kui üks lausetest on väär,
on ka And-lause väär.
2<3 && 1==1 ---> True
x || y || z
ehk Or[x, y, z,
]
Loogiline
või. Annab tõese väärtuse, kui vähemalt
üks lausetest x,
y, z,
on tõene. Kui
kõik laused on väärad, on ka Or-lause väär.
1==2||2==3||1==1 ---> True
Xor[x, y, z,
]
Loogiline välistav või. Annab väärtuse True,
kui paaritu arv lausetest x, y, z,
on tõesed
ja ülejäänud väärad. Xor-lause annab
väärtuse False, kui paarisarv lausetest on tõesed
ja ülejäänud väärad.
Xor[1==1,2==2] ---> False
Implies[x, y] Loogiline
järeldamine,
x
Þ y.
Annab väärtuse False, kui x on tõene ja
y
väär ning väärtuse True kõigil muudel
juhtudel.
Implies[1==0,2==2] ---> True
Loogikateheteid kasutatakse keerulisemate tingimuste koostamisel, vaata
näide 1 järgmises paragrahvis.
§7. LOKAALSED MUUTUJAD
Mathematica säilitab mälus kõigi töösessiooni
jooksul arvutatud muutujute väärtused. Mõnikord on otstarbekas
kasutada ajutisi, lokaalseid muutujaid, mida hoitakse alles ainult teatud
aeg. Seejärel nad kustutakse, säästes sellega nii arvuti
kui ka kasutaja mälu. Üks võimalus lokaalsete muutujatega
töötamiseks on Module-struktuur ehk moodul.
Module[{x, y,
},
laused]
Siin
x,
y,
on lokaalsed muutujad, mida kasutatakse ainult mooduli
lausetes.
Pärast
lausete täitmist muutujaid
x,
y,
ei säilitata.
Module[{x = x0,
y
=
y0,
},
laused]
Lokaalsetele
muutujatele omistatakse algväärtused.
Näide 1. Kui kolmnurga külgede pikkused on a,
b
ja c, siis tema pindala saab arvutada Heroni valemiga  ,
kus p = (a + b + c)/2.
,
kus p = (a + b + c)/2.
Koostame funktsiooni, mis arvutaks selle valemi järgi kolmnurga
pindala. Funktsiooni argumentideks on küljed a, b ja
c,
suurus p sobiks aga võtta lokaalseks muutujaks. Selleks,
et arvud a, b ja c saaksid olla kolmnurga külgedeks,
peavad nad olema positiivsed, samuti peab iga kahe külje summa olema
suurem kui kolmas külg. Et need nõuded oleksid täidetud,
kasutame tingimuslikku omistamist.
In[1]:=
Pindala[a_, b_, c_] := Module[{ p=(a+b+c)/2},
Sqrt[ p(p-a)(p-b)(p-c)] ]/;
a>0 && b>0 && c>0 &&
a+b>c && b+c>a && a+c>b
Vaatame, kuidas funktsioon töötab.
In[2]:=
Pindala[8,15,17]
Out[2]=
60
Näide 2. Kahe vektori 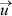 =
(u1;
u2;
u3) ja
=
(u1;
u2;
u3) ja 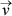 = (v1;
v2;
v3) vektorkorrutist
arvutatakse valemiga
= (v1;
v2;
v3) vektorkorrutist
arvutatakse valemiga
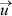 ×
× 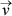 =
= 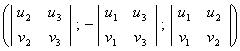 .
.
Vektorkorrutise koordinaatideks on vektoritest 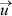 ja
ja 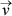 moodustatud
maatriksi teist järku miinorid õiges järjekorras võetuna.
Maatriksi miinoreid saab leida vastava korraldusega.
moodustatud
maatriksi teist järku miinorid õiges järjekorras võetuna.
Maatriksi miinoreid saab leida vastava korraldusega.
Minors[maatriks, n]
Leiab
maatriksi
n
järku miinorid.
Maatriksi 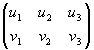 teist järku miinorid oleksid:
teist järku miinorid oleksid:
In[3]:=
Minors[{{u1,u2,u3}, {v1,v2,v3}}, 2]
Out[3]=
{{-(u2 v1) + u1 v2, -(u3 v1) + u1 v3,
-(u3 v2) + u2 v3}}
Koostame funktsiooni Cross (lühend sõnast cross
product), mis arvutab kahe vektori vektorkorrutise.
In[4]:=
Cross[ u_?VectorQ /; Length[u]==3,
v_?VectorQ /; Length[v]==3 ] :=
Module[{ m = Minors[{u,v},2][[1]] },
{m[[3]], -m[[2]], m[[1]]} ]
Funktsioonil on kaks argumenti, u ja v. Argumendi
mall u_?VectorQ kontrollib, et u oleks vektor, tingimus /;Length[u]==3
nõuab, et vektoril oleks kolm koordinaati. Samuti kontrollitakse
v sobivust. Funktsiooni lauseosa koosneb ühest moodulist, kusjuures
lokaalseks muutujaks on loend m. Korraldus Minors[{u,v},2][[1]]
leiab
vektoritest u ja v moodustatud maatriksi teist järku
miinorid. Need miinorid õiges järjekorras võetuna ongi
vektorkorrutise koordinaatideks.
Kontrollime, kuidas funktsioon töötab:
In[5]:=
Cross[{-1,4,2}, {4,-3,0}]
Out[5]=
{6, 8, -13}
Mõnikord võib vaja minna ka lokaalseid konstante. Sel
juhul sobib kasutada struktuuri
With[{x = x0,
y
=
y0,
},
laused]
Üldiselt võib lokaalseid konstante sisse tuua ka
Module abil, kuid With
esiteks töötab mõnevõrra
kiiremini ja teiseks rõhutab, et tegemist on just nimelt konstantidega.
§8. PROGRAMMIFAILIDE
KASUTAMISEST
Programmifailid ehk packaged pakuvad kasutajale täiendavaid
funktsioone ja korraldusi vähem tuntud, spetsiifiliste probleemide
lahendamiseks. Kui on tegemist ülesandega, mille lahendamiseks ei
ole sobivat käsku Mathematica võtmesõnade hulgas,
siis tasub seda otsida programmifailidest.
Programmifailid paiknevad üldjuhul omaette kataloogis. Kui Mathematica
kataloog on c:\wnmath22, siis programmide kataloog on tõenäoliselt
c:\wnmath22\packages. Viimane on omakorda jagatud temaatilisteks alamkataloogideks.
Programmifaili laiend on .m . Neid saab lugeda ja redigeerida
samuti nagu tööfaile. Programmifail sisaldab ainult programmi
teksti, seal ei ole väljundridu ega muid keerukaid struktuure. Seetõttu
võib package lugemiseks ja parandamiseks kasutada ka näiteks
Windowsi Notepadi või MS-DOSi Editori.
Laiemaks kasutamiseks mõeldud programmifail algab informeeriva
osaga, kus antakse teavet selle pealkirja, sisu, autorite ja muu olulise
kohta. Seal esitatakse ka packages defineeritud funktsioonide ja
käskude süntaks ning vajalikud selgitused.
Programmifaili kasutamiseks tuleb see kõigepealt arvuti mälusse
lugeda. Selleks on mitmeid võimalusi.
Näide 1. Võtame näiteks package, mis
kannab nime Statistics`ContinuousDistributions` ja mis sisaldab
mitmesuguseid statistilisi funktsioone tööks pidevate jaotustega.
Nagu nimi ütleb, paikneb vastav fail alamkataloogis ...\packages\statistics\.
Package
saab mälusse lugeda käsuga:
In[1]:=
<<Statistics`ContinuousDistributions`
Sümboli ` saab tekitada klahvikombinatsiooniga [Alt]+096.
Sama moodi oleks selle programmi saanud laadida käsuga
<<C:\wnmath22\packages\statisti\continuo.m
Esimises variandis kasutatakse package Mathematica-pärast
nimetust, teises kirjeldatakse faili loogiline asukoht kataloogipuus. Sobib
kasutada mittestandardsete programmide laadimiseks. Esimest varanti iseloomustavad
täispikad sõnad ning suurtäht iga sõna alguses,
teises on kataloogide ja failide nimed üldjuhul lühendatud mitte
enam kui kaheksatähelisteks, suur- ja väiketähti võib
kasutada suvaliselt.
Kolmas võimalus programmi laadimiseks on korraldus
In[2]:=
Needs["Statistics`ContinuousDistributions`"]
Sel juhul kontrollitakse, kas package on juba varem laaditud
ja kui on, siis teist korda seda enam ei tehta. Mõned packaged
annavad veateateid, kui neid mitu korda laadida.
Seda, kas programmi laadimine õnnestus, saab kontrollida korraldusega
$Packages, mis annab infot kõigi antud töösessiooni
jooksul laaditud
packagete kohta.
In[3]:=
$Packages
Out[3]=
{Statistics`InverseStatisticalFunctions`,
Statistics`Common`DistributionsCommon`,
Statistics`DescriptiveStatistics`,
Statistics`NormalDistribution`,
Statistics`ContinuousDistributions`,
Global`, System`}
Saime üsna pika nimekirja, sest meie pidevate jaotuste package
vajab oma töös ka mitmeid teisi programme, mis seetõttu
laetakse automaatselt. Kaks viimast nimetust Global` ja System`
ei ole programmifailid.
Pärast package laadimist saab kõiki seal defineeritud
funktsioone kasutada samuti kui Mathematica tuuma funktsioone. Kuidas
nende kohta infot saada? Kui puudub vastav kirjandus, tuleb programmifail
mingi vahendi (Mathematica või ka Winodowsi Notepad'iga)
lahti võtta ja lugeda selgitusi, mis hea tava kohaselt iga package
algusesse kirjutatakse. Juhul kui vajaliku funktsiooni nimi on teada, saame
tema kohta küsida infot traditsioonilisel moel, näiteks
In[4]:=
?NormalDistribution
Out[4]=
NormalDistribution[mu, sigma] represents the Normal (Gaussian)
distribution with mean mu and standard deviation sigma.
Eelmine
peatükk
Järgmine
peatükk
Sisukord


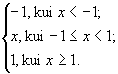

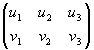 teist järku miinorid oleksid:
teist järku miinorid oleksid: