§1. KAHEMÕÕTMELINE GRAAFIKA

---

1.1. Primitiivid

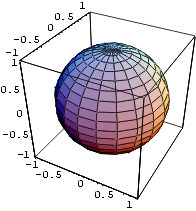
    Point[{x, y}] — Punkt koordinaatidega (x; y).
    Line[{{x₁, y₁}, {x₂, y₂},…}] — Murdjoon läbi punktide (x₁; y₁), (x₂; y₂), … .
    Polygon[{{x₁, y₁}, {x₂, y₂},…}] — Hulknurk tippudega (x₁; y₁), (x₂; y₂), … .
    Rectangle[{x₁, y₁}, {x₂, y₂}] — Ristkülik vastastippudega (x₁; y₁) ja (x₂; y₂).
    Circle[{x, y}, r] — Ringjoon keskpunktiga (x; y) ja raadiusega r.
    Disk[{x, y}, r] — Ring keskpunktiga (x; y) ja raadiusega r.
    Raster[maatriks] — Halltoonides raster e. ruudukeste masiiv.
    RasterArray[maatriks] — Värviline raster.
    Text[avaldis, {x, y}] — Teksti kirjutamine joonisele.
    PostScript[„string1”, „string2”,…] — PostScripti koodi kasutamine.

Esimesed kuus primitiivi on suhteliselt lihtsad ja toodud selgitustele on nende korral väga vähe lisada. Seetõttu peaks nende kasutamine olema arusaadav järgmises punktis toodud näidete abil. Rastritest ja tekstist räägime edaspidi pikemalt, PostScripti koodi tööpõhimõtteid aga antud juhendis selgitama ei hakkaks.

Kahemõõtemelise joonise jaoks koostatakse graafikaavaldis käsuga Graphics, mille üldkuju on:
Graphics[{primitiiv1, primitiiv2, …}] See korraldus teostab kõik vajalikud arvutused, kuid ei too joonist ekraanile. Et tulemust näha, läheb lisaks tarvis käsku Show. Kuidas seda konkreetselt teha, sellest allpool. Käsuga Graphics saab kasutada suuremat osa Plot-käsu juures toodud parameetritest. Erandiks on PlotStyle, PlotPoints ja veel mõned ainult graafiku joonestamisel mõtet omavad parameetrid.

1.2. Näiteid primitiivide kasutamisest

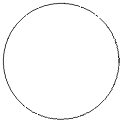
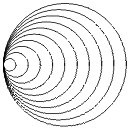
Näide 2. Joonestame 10 ringjoont, mille raadiused on 1, 2, … , 10 ja keskpunktid vastavalt (1; 0), (2; 0), … , (10; 0). Ringjoonte loendi koostame käsu Table abil. Ringjoonte keskpunkt ja raadius määratakse muutuja i abil, mis omandab väärtusi 1, 2, … , 10.
    In[3]:=   Table[Circle[{i,0},i],{i,0,10}]
    Out[3]=  {Circle[{1, 0}, 1], Circle[{2, 0}, 2],
            Circle[{3, 0}, 3], Circle[{4, 0}, 4],
            Circle[{5, 0}, 5], Circle[{6, 0}, 6],
            Circle[{7, 0}, 7], Circle[{8, 0}, 8],
            Circle[{9, 0}, 9], Circle[{10, 0}, 10]}

In[4]:=  Show[Graphics[%3], AspectRatio->Automatic]

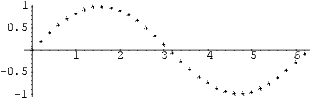
Näide 3. Kujundame punktidest siinusfunktsiooni graafiku. Koostame käsu Table abil punktide loendi ja anname talle nimeks pts (lühend inglisekeelsest sõnast points, sageli kasutatav muutujanimi). Muutuja x, mis on punkti x-koordinaadiks, omandab väärtusi 0; 0,2; 0,4; … .
    In[5]:=  pts = Table[ Point[{x,Sin[x]}],
             {x, 0, 2 Pi, 0.2 }];
Kuna eelmine rida lõppes semikooloniga, siis punktide loendit ekraanile ei trükitud. Et tulemusest ettekujutust saada, küsime loendi nelja esimese elemendi väärtust.
    In[6]:=  pts[[{1,2,3,4}]]
    Out[6]= {Point[{0, 0}], Point[{0.2, 0.198669}],
           Point[{0.4, 0.389418}],
           Point[{0.6, 0.564642}]}

    In[7]:=  Show[ Graphics[pts],
            Axes->True,
            AspectRatio->Automatic]

Näide 4. Teame, et väljend Circle[{x,y},r] annab ringjoone keskpunktiga (x, y) ja raadiusega r. Käsuga Circle saab joonestada ka ellipseid ja ringjoonte ning ellipsite kaari.

Circle[{x, y}, {a, b}] Ellips keskpunktiga (x; y) ning pooltelgedega a ja b.
Circle[{x, y}, r, {a , b }] Ringjoone kaar, mille algnurk on a ja lõppnurk b . Nurgad a ja b esitatakse radiaanides. Nurki mõõdetakse x-telje positiivsest suunast vastupäeva.
Circle[{x, y}, {a, b}, {a , b }] Nurkade a ja b vahele jääv ellipsi kaar.
Analoogiliselt primitiiviga Circle saab primitiiviga Disk joonestada seest värvitud ellipseid ja ringide ning ellipsite sektoreid.

Joonestame 15 ellipsit, millel on ühine keskpunkt, kuid pooltelgede pikkused on erinevad. Olgu esimese pooltelje pikkused 1, 2, … , 15 ja teise pooltelje pikkused vastavalt 15, 14, … , 1.
    In[8]:=  Table[ Circle[{0,0},{i,16-i}], {i,1,15}];
    In[9]:=  Show[Graphics[%8],AspectRatio->Automatic]

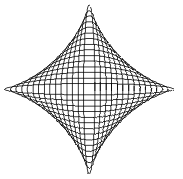
Saab tõestada, et selle ellipsite parve mähisjooneks on astroid.

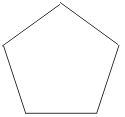
Näide 5. Joonestame korrapärase viisnurga. Arvutame viisurga tippude koordinaadid, lähtudes ringjoone parameetrilistest võrranditest x = sin t, y = cos t, kui t muutub sammuga 2p /5. Et saada kinnist murdjoont, peab punktide loendi viimane element olema sama, mis esimene element.
    In[10]:=  pts = Table[{N[Sin[t]],N[Cos[t]]},
            {t,0,2 Pi,2 Pi/5}]
    Out[10]= {{0, 1.}, {0.951057, 0.309017},
            {0.587785, -0.809017}, {-0.587785, -0.809017},
            {-0.951057, 0.309017}, {0, 1.}}

    In[11]:=  Show[ Graphics[Line[pts],
               AspectRatio->Automatic]]

Muudame punktide järjekorda.
    In[12]:=  pts1 = pts[[{1,3,5,2,4,6}]]
    Out[12]=  {{0, 1.}, {0.587785, -0.809017},
             {-0.951057, 0.309017}, {0.951057, 0.309017},
             {-0.587785, -0.809017}, {0, 1.}}
    In[13]:=  Show[Graphics[Line[pts1],
             AspectRatio->Automatic]]

Joonestame loendite pts ja pts1 abil kaks hulknurka.
    In[14]:=  Show[ Graphics[Polygon[pts],
              AspectRatio->Automatic]]

    In[15]:=  Show[ Graphics[Polygon[pts1],
             AspectRatio->Automatic]]

1.3. Teksti kirjutamine joonisele

Näide 6. Kirjutame joonisele teksti "Sin[x]/(x+1)" ja seejärel võrdluseks sama teksti ilma jutumärkideta.
    In[16]:=  Show[Graphics[{Text["Sin[x]/(1+x)",{1,2}],
                          Text[ Sin[x]/(1+x) ,{1,1}]},
                     Axes->True,
                     PlotRange->{0,3} ]]

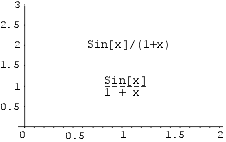
Kirja fonti ja suurust on võimalik muuta korraldusega FontForm.
Text[FontForm[avaldis, {"font", suurus}], {x, y}] Määratud kirjasuurus säilib joonise suurendamisel ja vähendamisel, s. t. et teksti suurus ei muutu proportsionaalselt joonise ülejäänud mõõtmetega. Kui tekst ei mahu joonisele ära, aitab mõnikord joonise suurendamine (hiirega). Teine võimalus on vähendada kirja suurust.
Mathematica verisiooni 2.2 korral ei ole võimalik kasutada neid fonte, mille nimetus koosneb mitmest sõnast, näiteks Monotype Corsiva, Century Gothic. Mõnede fontide (Times, Helvetica, Courier) korral saab kasutada kaldkirja ja rasvast kirja. Selleks tuleb fondi nimi esitada kujul "nimi-Bold", "nimi-Italic" või "nimi-BoldItalic".

Näide 7.
    In[17]:=  Show[ Graphics[{
          Text[FontForm[ "See on Frankensteini font", {"Frankenstein",12}],{0,1}],
          Text[FontForm[ "aga see Timesi kursiiv", {"Times-Italic",12}],{0,-1}]},
           Axes->True,
           PlotRange->{-2,2}]]

1.4. Direktiivid

    GrayLevel[g] — Objekti värv, määratakse hallskaalas.
    RGBColor[r, g, b] — Värv, määratakse RGB-värvimudeli alusel.
    CMYKColor[c, m, y, k] — Värv, määratakse CMYK-värvimudeli alusel.
    Hue[h], aga ka Hue[h, s, b] — Värv, määratakse HSB-värvimudeli alusel.
    Dashing[{d₁, d₂,…}] — Kriipsjoon, pikkused antakse suhtelistes ühikutes.
    AbsoluteDashing[{d₁, d₂,…}] — Kriipsjoon, kasutatakse absoluutset pikkusühikut.
    Thickness[d] — Joone jämedus suhtelisestes ühikutes.
    AbsoluteThickness[d] — Joone jämedus absoluutsetes ühikutes.
    PointSize[s] — Punkti raadius suhtelistes ühikutes.
    AbsolutePointSize[s] — Punkti raadius absoluutsetes ühikutes.

Direktiivid tuleb loetleda enne primitiive, millele neid rakendada tahetakse. Graafikaavaldise üldkuju on sel juhul:
    Graphics[{direkt1, direkt2, …, prim1, prim2,…}]
Üldjuhul mõjub iga direktiiv ainult temale järgnevatele primitiividele. Näiteks kirjutise
    Graphics[{prim1, direkt1, prim2}]
korral rakendatakse direktiivi direkt1 ainult teisele primitiivile prim2.
Üksikute primitiivide omaduste määramiseks võib kasutada loogelisi sulge, näiteks
    Graphics[{direkt1, {direkt2, prim1}, prim2}]
Siin mõjub direktiiv direkt1 mõlemale graafikaprimitiivile, direktiiv direkt2 aga ainult primitiivile prim1.

1.5. Värvid

GrayLevel[g] Võimaldab värvida objekte erinevates halltoonides. Siin g on reaalarv 0 ja 1 vahelt ning mida suurem on g, seda heledamat halli kasutatakse.
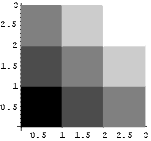
Näide 8. Joonestame kolm ringi, mille raadiused on 1, 2 ja 3 ühikut ja värvime nad erinevates halltoonides.
    In[18]:=  Show[Graphics[{
            GrayLevel[0.8], Disk[{0,0},3],
            GrayLevel[0.5], Disk[{0,0},2],
            GrayLevel[0],  Disk[{0,0},1]},
           AspectRatio->Automatic]]

RGBColor[r, g, b] Sellest direktiivist oli juba juttu punktis 2.5.1. seoses funktsiooni graafikute joonestamisega. Kõik seal öeldu jääb käesolevas punktis kehtima, kaasaarvatud värviselektori kasutamine. Meenutame, et RGBColor määrab objekti värvi RGB-värvimudeli, s. o. põhivärvide punane, roheline ja sinine alusel. Värvitoon segatakse kokku kolme värvikomponendi r, g ja b põhjal.
    r – red – punane;
    g – green – roheline;
    b – blue – sinine.
Komponendid r, g ja b on reaalarvud 0 ja 1 vahelt. Mida suurem on arv, seda rohkem vastavat värvikomponenti lisatakse.

Näide 9. Vaatame, kuidas muutub värvitoon, kui punane komponent muutub 0-st 1-ni, roheline ja sinine komponent on aga nullid. Joonestame üksteise kõrvale 40 ristkülikut. Iga ristküliku värvi määrab direktiiv RGBColor[i,0,0], kusjuures i muutub vasakult paremale liikudes 0-st 1-ni sammuga 1/39. Ristkülikute loendi koostame käsuga Table. Lõpuks joonestame saadud värviriba ümber raamjoone.
    In[19]:=  Show[ Graphics[{
             Table[
             {RGBColor[i/39,0,0], Rectangle[{i,0},{i+1,8}]},{i,0,39}],
             Line[{{0,0},{40,0},{40,8},{0,8},{0,0}}] },
           AspectRatio->Automatic]]

CMYKColor[c, m, y, k] Määrab objekti värvi CMYK-värvimudeli alusel. Värvitoon segatakse kokku nelja komponendi c, m, y ja k põhjal.
    c – cyan – tsüaan, helesinine;
    m – magneta – magneta, lilla;
    y – yellow – kollane;
    k – black – must.
Kõik komponendid on reaalarvud 0 ja 1 vahelt. Mida suurem on arv, seda rohkem vastavat värvikomponenti lisatakse. Näiteks
    CMYKColor[0,0,1,0] kollane;
    CMYKColor[1,0,1,0] heleroheline;
    CMYKColor[0,0,0,0] valge;
    CMYKColor[0,0,0,1] must.

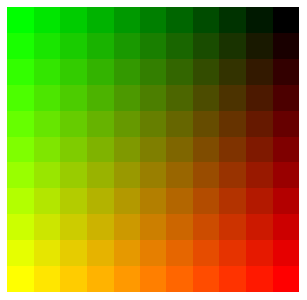
Hue[h] Määrab objekti värvi vastavalt värviringile. Kui arv h muutub 0-st 1-ni, siis värvitoon Hue[h] muutub punasest üle kollase, rohelise, sinise ja lilla jälle punaseks. Ühest suuremate h väärtuste korral hakatakse neid värve tsükliliselt kordama.
Hue[h, s, b] Värvitooni saab täpsustada suuruste s ja b abil.
s – saturation – küllastatus;
b – brightness – heledus, s ja b on reaalarvud piirkonnst [0; 1].
Hue[h] annab sama tulemuse kui Hue[h,1,1].
Seda, kuidas küllastatuse ja heleduse muutmine värvitoonile mõjub, võib uurida eelmises näites toodud värviribasid joonistades. Näiteks värvide ülemineku valgest punaseni saame direktiiviga Hue[0,i,1], (i muutub 0-st 1-ni) ja ülemineku mustast punaseni direktiiviga Hue[0,1,i].

1.6. Rastrid

1.7. Joone jämedus, kriipsjoon ja punkti suurus

Absoluutsetel ja suhtelistel ühikutel on üks oluline erinevus. Jooned, mille jämedus on määratud suhtelistes ühikutes, muutuvad joonise vähendamisel või suurendamisel vastavalt peenemaks või jämedamaks. Jooned, mille jämedus on määratud absoluutsetes ühikutes, säilitavad oma laiuse. See tähendab, et joonise suurendamisel (vähendamisel) joonte jämedus ei muutu proportsionaalselt ülejäänud mõõtudega.

Niisamuti on punkti suurust ja kriipsjoone kriipsude pikkust võimalik määrata kas absoluutsetes või suhtelistes ühikutes.
Dashing[{d}] Objektide joonestamisel kasutatakse kriipsjoont, kus ühe kriipsukese pikkus on d. Tühikute pikkus kriipsude vahel on samuti d. Pikkus d määratakse murdosana kogu joonise laiusest.
Dashing[{d₁, d₂, d₃, …, d_n}] Kriipsude ja tühikute pikkust muudetakse tsükliliselt. Esimese kriipsu pikkus on d₁ , esimese tühiku pikkus d₂ , teise kriipsu pikkkus d₃ , teise tühiku pikkus d₄ jne. (n + 1)-se kriipsu (või tühiku) pikkus on jälle d₁.
Dashing[{}] Pidev joon.
AbsoluteDashing[{d₁, d₂, …}] Kriipsjoone kasutamine. Kriipsukeste pikkust mõõdetakse absoluutsetes pikkusühikutes.
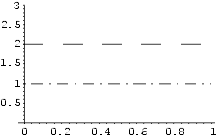
Näide 11. Joonestame kaks kriipsjoont. Olgu esimesel nii kriipsude kui tühikute suhteline pikkus 1/10, teisel kriipsude pikkus vaheldumisi 0,01 ja 0,06 ning tühikute pikkus 0,03.
    In[24]:=  Show[ Graphics[{
                Dashing[{1/10}],  Line[{{0,2},{1,2}}],
                Dashing[{0.01,0.03,0.06,0.03}],  Line[{{0,1},{1,1}}]},
             Axes->True,
             PlotRange->{0,3}]]

PointSize[r] Määrab järgnevate punktide raadiuse. Raadius määratakse murdosana kogu joonise laiusest. Kahemõõtmelise graafika korral on r vaikimisi väärtuseks 0,008.
AbsolutePointSize[r] Määrab joonisele kantavate punktide raadiuse. Raadiust mõõdetakse absoluutsetes mõõtühikutes.

1.8. Plot, ParametricPlot ja primitiivid

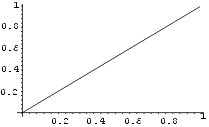
Plot-käsu väljundit saab kasutada uute jooniste tegemisel.

Näide 13. Eelmises väljundis on ainult üks graafikaprimitiiv — Line. Võtame punktid, mida see joon läbib ja asendame iga punkti (x; y) joonega punktide (x; 0) ja (x; y) vahel. Seda on lihtne teha asendamisreegli (replacement rule) abil. Asendamisreeglitest on pikemalt kirjutatud järgmise peatüki 3. paragrahvis.
    In[27]:=  %26[[1,1,1,1]] /. {x_,y_} -> Line[{{x,0},{x,y}}];
Esitame uue joonise.
    In[28]:=  Show[ Graphics[%27], Axes->True]

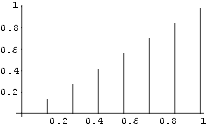
    Out[28]=  -Graphics-
 

§2. KOLMEMÕÕTMELINE GRAAFIKA

---

2.1. Primitiivid

Point[{x, y, z}] — Punkt koordinaatidega (x; y, z).
Line[{{x₁, y₁, z₁}, {x₂, y₂, z₂}, …}] — Murdjoon, mis läbib punkte (x₁ ; y₁ ; z₁), (x₂ ; y₂ ; z₂), … .
Polygon[{{x₁, y₁, z₁}, {x₂, y₂, z₂}, …}] — Hulknurk tippudega (x₁ ; y₁ ; z₁), (x₂ ; y₂ ; z₂), … .
Cuboid[{x₁, y₁, z₁}, {x₂, y₂, z₂}] — Risttahukas, mille tahud on paralleelsed koordinaattasanditega ja kaks vastastippu on punktides (x₁ ; y₁ ; z₁) ja (x₂ ; y₂ ; z₂).
Text[avaldis, {x, y, z}] — Tekst keskpunktiga (x; y, z).

Ruumilise joonise jaoks koostatakse graafikaavaldis käsuga Graphics3D, mille üldkuju on
Graphics3D[{prim1, prim2, …}] See korraldus teostab joonise jaoks vajalikud arvutused. Joonise saab ekraanile tuua käsuga Show.
Primitiivid Point, Line, Polygon ja Text on analoogilised vastavate kahemõõtmeliste objektidega. Toome ühe näite kolmemõõtmelise joonise koostamisest.
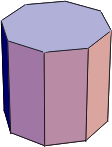
Näide 1. Joonestame korrapärase 8-tahulise püstprisma. Tähistame tahkude arvu muutujaga n. Nii on võimalik n väärtust muutes hõlpsasti joonestada suvalise arvu tahkudega prismasid.
    In[1]:=  n = 8;
Arvutame prisma alumise ja ülemise tahu tippude koordinaadid.
    In[2]:=   pts1 = Table[ {Cos[i],Sin[i],0}, {i,0,2 Pi,2 Pi/n}];
           pts2 = Table[ {Cos[i],Sin[i],2}, {i,0,2 Pi,2 Pi/n}];
Prisma külgtahud saame, kui rakendame sobivalt valitud tippudele graafika primitiivi Polygon.
    In[3]:=  kyljed = Table[
                Polygon[{pts1[[i]], pts2[[i]],
                pts2[[i+1]], pts1[[i+1]] }],
            {i,1,n}];
Käsuga Graphics3D koostame joonise. Ilusama tulemuse saamiseks jätame parameetriga Boxed->False ära kasti, mis kolmemõõtmelist joonist vaikimisi ümbritseb, parameetriga ViewPoint muudame vaatepunkti.
    In[4]:=  Show[ Graphics3D[
               {Polygon[pts1], Polygon[pts2], kyljed},
            Boxed->False,
            ViewPoint->{1.3,-6.7,4.2}]]

2.2. Direktiivid

EdgeForm[{direktiiv(id)}] Võimaldab muuta hulknurga äärejoonte ilmet. EdgeForm’iga antud direktiive rakendatakse hulknurga äärejoontele, nii nagu oleks tegemist objektiga Line.
EdgeForm[] Hulknurgale ei joonestata äärejoont.
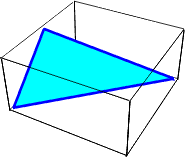
Näide 3. Joonestame helesinise kolmnurga tumesinise äärejoonega. Et oleksid näha loomulikud värvid, keelame parameetriga Lighting->False valgustuse.
    In[6]:= Show[ Graphics3D[
            {RGBColor[0,1,1],
             EdgeForm[{RGBColor[0,0,1],Thickness[0.01]}],
             Polygon[{{0,0,0},{0,1,1},{2,2,0}}]},
           Lighting->False]]

FaceForm[direkt1, direkt2] Hulknurga esikülg värvitakse nii, nagu määrab direktiiv direkt1, tagakülg aga nii, nagu määrab direkt2. Direktiivid direkt1 ja direkt2 peavad olema kas värvid GrayLevel, Hue, RGBColor, CMYKColor või siis direktiiv SurfaceColor. Kõik värvimäärangud, mis on antud ilma FaceForm’ita, kehtivad hulknurga mõlema poole jaoks.
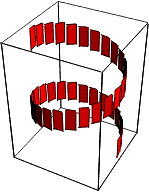
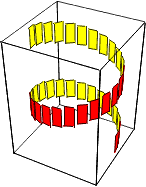
Näide 4. Koostame ristkülikutest spiraali s. Ristkülikute esikülje värvime punaseks, tagakülje kollaseks.
    In[7]:=  s = Table[
             Polygon[
              {{Cos[t], Sin[t], t/4},
               {Cos[t+0.2], Sin[t+0.2], t/4},
               {Cos[t+0.2], Sin[t+0.2], (t+2)/4},
               {Cos[t], Sin[t], (t+2)/4}}],
            {t, 0, 3 Pi, Pi/12}];
    In[8]:=  Show[ Graphics3D[
               {FaceForm[ RGBColor[1,0,0], RGBColor[1,1,0]], s},
            Lighting->False]]

SurfaceColor[direkt] Hulknurga värvi määramine. Kõigis eelmistes näidetes, kus oli tegemist värviliste hulknurkadega, kasutasime parameetrit Lighting->False. Põhjuseks oli asjaolu, et kui valgustus on sisse lülitatud (Lighting->True), siis värvitakse hulknurk vastavalt tema pinnale langevale valgusele, värvidirektiive aga ei arvestata. Direktiiviga SurfaceColor määratud värvi võetakse arvesse ka siis, kui valgustus on sisse lülitatud. Sel juhul leitakse hulknurga lõplik värvitoon valguse SurfaceColor’iga antud värvi summana. Surfacecolor’iga saab muuta ka pinna peegeldamisomadusi, kuid seda me siin pikemalt ei käsitle.
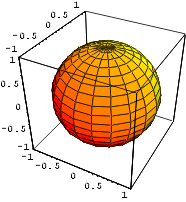
Näide 5. Joonestame veelkord eelmise näite spriaali, kuid ristkülikud värvime mõlemalt poolt punaseks. Kuna kasutame direktiive SurfaceColor[RGBColor[1,0,0]], siis jäävad mõned neist heledamad, teised tumedamad, sõltuvalt sellest, kuidas nad on valgustatud.
    In[9]:=  Show[ Graphics3D[
                {SurfaceColor[ RGBColor[1,0,0]], s}]]

2.3. Valgustusest

    Eelmine peatükk     Järgmine peatükk     Sisukord