Neljas peatükk käsitleb Mathematica rakendamist mõnede
kõrgemasse matemaatikasse kuuluvate ülesannete lahendamisel.
§1. DIFERENTSIAALVÕRRANDID
Diferentsiaalvõrrandeid saab lahendada analüütiliselt
või numbriliselt. Vastavad käsud on DSolve ja
NDSolve. Esimene leiab otsitava funktsiooni analüütilise
kuju, näiteks y(x) = x2 + 3 sin x.
Numbrilisel lahendamisel saab lahendfunktsiooni tabuleerida ja joonestada
tema graafikut, funktsiooni analüütilist kuju aga ei leita. Täiendavat
materjali diferentsiaalvõrrandite kohta võib leida raamatust
[10].
Peab ütlema, et diferentsiaalvõrrandite lahendamine ei
ole Mathematica kõige tugevam külg. On olemas tohutu
hulk lihtsalt lahenduvaid võrrandeid, mille lahendeid ta ei suuda
leida; nii et vastuse asemel veateate saamist tuleb lugeda pigem tüütuks
reegliks kui harvaesinevaks erandiks.
1.1. Diferentsiaalvõrrandite analüütiline lahendamine
DSolve[ difvõr, y[x],
x]
Lahendab
diferentsiaalvõrrandi analüütiliselt.
y[x]
on otsitav funktsioon ja x sõltumatu muutuja. Võrrandi
kirjapanemisel kasutatakse järgmist süntaksit:
-
Otsitav funktsioon y(x) - y[x] ;
-
tema esimene tuletis y'(x) - y'[x] ;
-
teine tuletis y''(x) - y''[x] ;
-
5. järku tuletis y(5)(x) - Derivative[5][y][x].
Mathematica help-fail väidab, et käsk DSolve lahendab
ka diferentsiaalvõrrandite süsteeme. Tegelikul lahendamisel
võivad tekkida tõrked. Vähemalt paketi versioon 2.2
väljastab võrrandisüsteemide analüütilisel lahendamisel
ainult veateateid.
-
Näide 1. Lahendame diferentsiaalvõrrandi y'
= 2x, kus y = y(x).
-
In[1]:= DSolve[ y'[x]==2x, y[x],
x]
-
Out[1]=
2
-
{{y[x] -> x + C[1]}}
-
C[1] - lahendamisel tekkiv määramata konstant. Võrrandi
lahendiks on seega funktsioon y(x) = x2
+ C1 .
-
Määramata konstandi tähist on võimalik parameetriga
DSolveCostants->const, mille vaikimisi väärtuseks
on C.
-
Toodud lihtsa võrrandi korral ei teki lahendi õigsuses kahtlust,
keerukamate võrrandite lahendeid aga tasub kontrollida, sest leidub
võrrandeid, mida Mathematica lahendab valesti.
-
Kontrolliks lahendfunktsioonist tuletis(t)e leidmisel saab kasutada väljundrida:
-
In[2]:= D[ y[x]/.%1, x]
-
Out[2]= {2 x}
DSolve[{difvõr, algtingimus1,...},
y[x],
x]
Leiab
diferentsiaalvõrrandi lahendi, mis rahuldab antud algtingimusi.
-
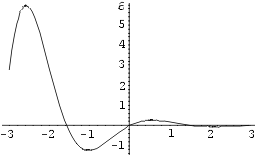
Näide 2. Lahendame diferentsiaalvõrrandi y''
+ 2y' + 5y = 0 tingimustel y(0) = 0 ja y'(0)
= 1. Joonestame leitud lahendi graafiku.
-
In[3]:= DSolve[{y''[x] + 2 y'[x] + 5 y[x]
== 0,
-
y[0]==0,
-
y'[0]==1}, y[x],x]
-
-
Out[3]=
Sin[2 x]
-
{{y[x] -> --------}}
-
x
-
2 E
Graafiku joonestame Plot-käsu abil. Leitud lahendfunktsiooni
võib uuesti sisestada, kuid võib kasutada ka väljundreal
olevat tulemust. Selleks tuleb funktsiooni asemel kirjutada Evaluate[y[x]/.%3]
.
-
In[4]:= Plot[ Evaluate[y[x]/.%3],
{x,-3,3}]
-
-
-
1.2. Integraalkõverate parve joonestamine
Lahendades diferentsiaalvõrrandit ilma algtingimusteta, on vahel
kasulik joonestada integraalkõverate parv, s. t. anda määramata
konstandile erinevaid väärtusi ja joonestada saadud funktsioonide
graafikud.
-
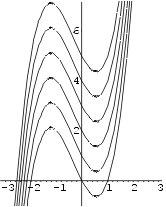
Näide 3. Lahendame diferentsiaalvõrrandi y' =
3x2 + 2x - 2 ja joonestame integraalkõverate
parve. Et määramata konstandile saaks anda väärtusi,
tuleb ta tähistada mingi C-st erineva tähega.
-
In[5]:= lah = DSolve[ y'[x]==3x^2+2x-2,
y[x], x,
-
DSolveConstants->K]
-
Out[5]=
2 3
-
{{y[x] -> -2 x + x + x +
K[1]}}
-
Koostame lahendfunktsioonide loendi, andes K[1]-le väärtusi
0-st 5-ni.
-
In[6]:= t = Table[ y[x]/.lah, {K[1],0,5}]
-
Out[6]=
2 3
2 3
-
{{-2 x + x + x }, {1 - 2 x + x + x },
-
2 3
2 3
-
{2 - 2 x + x + x }, {3 - 2 x + x + x },
-
2 3
2 3
-
{4 - 2 x + x + x }, {5 - 2 x + x + x }}
-
-
In[7]:= Plot[ Evaluate[t], {x,-3,3},
-
AspectRatio->Automatic,
PlotRange->{-1,7.2}]
-
-
-
1.3. Diferentsiaalvõrrandite numbriline lahendamine
NDSolve[{difvõr, algting1,...},
y,
{x, xmin,
xmax}]
Lahendab
diferentsiaalvõrrandi numbriliselt piirkonnas [xmin
; xmax]. Algtingimusi peab olema sama palju, kui suur
on kõige kõrgem võrrandis esindatud tuletise järk.
Algtingimused antakse tavaliselt kujul
y(x0)
= a1, y' (x0) = a2
jne.,
kuid võib kasutada ka keerulisemaid avaldisi. Punkt x0
ei pea tingimata kuuluma piirkonda [xmin ; xmax].
NDSolve
ei
esita lahendiks olevat funktsiooni analüütilisel kujul vaid arvuloenditena.
Neid arvuloendeid väljundreal ei esitata, näidatakse vaid piirkond,
kus võrrand on lahendatud. Väljundit kasutades on võimalik
arvutada funktsiooni väärtust piirkonna [xmin
; xmax] suvalises punktis, selles piirkonnas funktsiooni
tabuleerida ja joonestada tema graafikut.
-
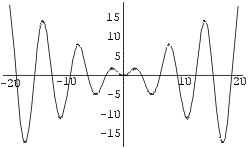
Näide 4. Lahendame numbriliselt diferentsiaalvõrrandi
x
cos x + sin x = y', kui y(p
) = 0. Leiame lahendi, kui x Î
[- 20; 20].
-
In[8]:= lah = NDSolve[{x Cos[x] + Sin[x]==y'[x],
y[Pi]==0},
-
y,{x,-20,20}]
-
Out[8]= {{y -> InterpolatingFunction[{-20.,
20.}, <>]}}
-
Leiame lahendfunktsiooni väärtuse kohal x = 3,52 .
-
In[9]:= y[3.52]/.lah
-
Out[9]= {-1.30043}
-
Joonestame funktsiooni y graafiku piirkonnas [- 20; 20].
-
In[10]:= Plot[ Evaluate[y[x]/.lah], {x,-20,20}]
-
NDSolve[{difvõr1, difvõr2,...,
algting1,...},{y,x,...},{t,tmin,tmax}]
Lahendab
numbriliselt diferentsiaalvõrranite süsteemi.
-
Näide 5. Lahendame võrrandisüsteemi
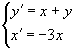 algtingimustel
algtingimustel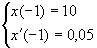 ja
ja 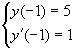 piirkonnas
[ - 2; 1].
piirkonnas
[ - 2; 1].
-
In[11]:= lah = NDSolve[{ y'[t]==x[t]+y[t],
x'[t]==-3 x[t],
-
x[-1]==10, y[-1]==5,
-
x'[-1]==0.05, y'[-1]==1},
-
{x,y}, {t,-2,1}]
-
-
Out[11]= {{x -> InterpolatingFunction[{-2.,
1.}, <>],
-
y -> InterpolatingFunction[{-2.,
1.}, <>]}}
Esitame lahendfunktsioonid tabelina. Olgu tabeli samm 0,4.
In[12]:= TableForm[
Table[
{t,x[t]/.lah,y[t]/.lah}, {t,-2,1,0.4}],
TableHeadings -> {None,{"t","x[t]","y[t]"}}]
Out[12]= t
x[t] y[t]
-
-2
200.856 -47.4549
-
-1.6
60.4966 -11.0081
-
-1.2
18.2212 1.58518
-
-0.8
5.48813 7.78849
-
-0.4
1.65299 13.2526
-
-16
-
-1.11022 10 0.497874
20.2626
-
0.4
0.149956 30.3765
-
0.8
0.0451659 45.3611
Parameeter TableHeadings->{{ridadepäised},{veergudepäised}}
lisab
tabeli ridadele ja veergudele pealkirjad.
Märkus. Kui see tabel väljastada TableFormi kasutamata,
on näha, et tabelis on liigseid alamloendeid. Kuna need praegu ei
sega, siis me neid ka ei eemalda.
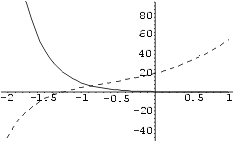
Joonestame leitud funktsioonide x = x(t) ja y
= y(t) graafikud ühes teljestikus. Et graafikuid eristada,
joonestame x(t) graafiku pideva joonega, y(t)
oma aga kriipsjoonega. Selleks anname parameetrile PlotStyle väärtuseks
graafika direktiivi Dashing, vt. p. 3.1.4. Parameetri väärtused
Dashing[{}] (pidev joon) ja Dashing[{0.02}]}] (kriipsjoon)
kehtivad vastavalt esimese ja teise graafiku jaoks.
-
In[13]:= Plot[ Evaluate[{x[t],y[t]}/.lah],
{t,-2,1},
-
PlotStyle -> {Dashing[{}],Dashing[{0.02}]} ]
-
-
-
1.4. Osatuletistega diferentsiaalvõrrandid
Kasutades Mathematica versiooni 2.2, tuleb osatuletistega diferentsiaalvõrrandite
lahendamiseks mällu lugeda package Calculus`PDSolve1`.
Versiooni 3.0 korral ei ole seda teha tarvis.
Osatuletistega diferentsiaalvõrrandeid lahendab harelike dif-võrrandite
juures juba kasutusel olnud korraldus DSolve. Süntaks on
sarnane:
DSolve[osatuldifvõr, u[x,
y],
{x,
y}]
Siin u[x,
y] on otsitav kahe muutuja
funktsioon ning x ja
y on sõltumatud muutujad. Võrrandi
kirjapanekul kasutatakse tähsitusi:
Otsitav funktsioon u = u(x;y) - u[x,y]
;
funktsiooni u 1. tuletis x-i järgi u'x
- D[u[x,y],x] ;
funktsiooni u 1. tuletis y-i järgi u'y
- D[u[x,y],y].
Hoiatus. Mathematica lahendab diferentsiaalvõrrandeid
suhteliselt halvasti, kuid osatuletistega diferentsiaalvõrrandeid
lahendab ta eriti halvasti.
-
Näide 6. Lahendame võrrandi
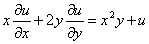 .
.
-
Esmalt laadime package Calculus`PDSolve1`, kui see on vajalik.
-
In[14]:= <<Calculus`PDSolve1`
-
Sümboli ` jaoks vajuta [Alt] + 096.
-
In[15]:= DSolve[
-
x D[u[x,y],x] + 2y
D[u[x,y],y] == x^2 y + u[x,y],
-
u[x,y],{x,y}]
-
Out[15]=
x y y
-
{{u[x, y] -> x (--- + C[1][--])}}
-
3 2
-
x
-
C[1] tähistab esimest järku osatuletistega diferentsiaalvõrrandi
lahendis esinevat määramata funktsiooni.
-
§2. INTERPOLEERIMINE
2.1. Newtoni interpolatsioonipolünoom
Interpoleerimise kohta võib lisamaterjali leida raamatust [11].
-
InterpolatigPolynomial[andmed, x]
Leiab
arvandmetele täpse interpolatsioonipolünoomi Newtoni kujul, kus
x
on polünoomi muutuja. n interpolatsioonisõlme korral
on tulemuseks (n - 1) astme polünoom. Andmed esitatakse kujul
-
{{ x1 , f(x1)
},{
x2
,
f(x2)
},...,{
xn
,
f(xn)
}}
või kujul
-
{ f(x1) , f(x2)
,...,
f(xn)
},
kui x1 = 1; x2 = 2; ...,
xn
= n.
-
Kui on teada funktsiooni tuletiste väärtused interpolatsioonisõlmedes,
siis võib iga f(xi) asendada loendiga
-
{
f(xi)
,
f'(xi)
,
f''(xi)
,...}
Näide 1. Koostame interpolatsioonipolünoomi tabeliga
| 1 |
2 |
3 |
4 |
5 |
6 |
| 10 |
22 |
26 |
12 |
10 |
15 |
antud funktsiooni jaoks.
-
In[1]:= data = {10, 22, 26, 12, 10,
15}
-
Out[1]= {10, 22, 26, 12, 10, 15}
-
-
In[2]:= poly1 = InterpolatingPolynomial[data,
x]
-
Out[2]=
5 5 5 (-5 + x)
-
10 + (12 + (-4 + (-(-) +
(- - ----------) (-4 + x))
-
3 3 8
-
-
(-3 + x)) (-2 + x)) (-1
+ x)
-
-
Interpolatsioonipolünoomi võib esitada ka teistsugusel kujul.
-
In[3]:= Expand[ poly1 ]
-
Out[3]=
2 3
4 5
-
2987 x 4919 x 1715 x 265
x 5 x
-
115 - ------ + ------- -
------- + ------ - ----
-
12 24
24 24
8
-
Näite illustreerimiseks joonestame interpolatsioonipolünoomi
graafiku. Samale joonisele kanname ka andmetabelile vastavad punktid ja
ühendame nad murdjoonega.
-
In[4]:= g1 = Plot[ poly1{x,1,6},
DisplayFunction->Identity];
-
p = ListPlot[ data, PlotStyle->PointSize[0.03],
DisplayFunction->Identity];
-
j = ListPlot[ data, PlotJoined->True,
DisplayFunction->Identity];
-
-
Show[g1, p, j, DisplayFunction->$DisplayFunction]
-
-
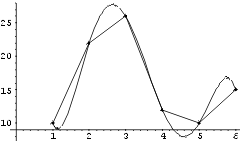
-
2.2. Vähimruutude meetod
-
Fit[andmed, funktsioonid,
muutujad]
Leiab
andmetele lähendfunktsiooni vähimruutude meetodil. Leitav lähend
on lineaarkombinatsioon kasutaja poolt ette antud funktsioonidest, mis
üldiselt ei pea olema astmefunktsioonid. Käsku Fit saab
kasutada ka mitme muutuja funktsioonide lähendamiseks. Andmed esitatakse
kujul
-
{{ x1 , y1,
..., f(P1) },{
x2
,
y2,
..., f(P2)
},...,{
xn
,
yn,
...,
f(Pn)
}},
kus Pi = (xi , yi ,
...).
-
Kui tegemist on ühe muutuja x funktsiooniga ja x omandab
väärtusi 1, 2, ... , n, siis võib kasutada kirjutust
-
{ f(x1) , f(x2)
,
..., f(xn) }.
-
Käsu viimases osas tuleb loetleda kõik muutujad. Kui muutujaid
on rohkem kui üks, siis tuleb nad esitada loendina. Muutujate arv
peab olema võrdne koordinaatide x, y, . . . arvuga
andmetabelis.
-
-
Näide 2. Leiame eelmises näites toodud andmetabelile lähendfunktsiooni,
mis oleks lineaarkombinatsioon funktsioonidest 1, x, x2
ja x3.
-
In[5]:= poly2 = Fit[ data, {1, x,
x^2, x^3}, x]
-
Out[5]=
2 3
-
-30. + 55.0913 x - 17.0952 x +
1.52778 x
-
-
Joonestame interpolatsioonipolünoomi graafiku.
-
In[6]:= g2 = Plot[ poly2, {x,1,6}]
-
-
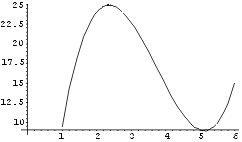
-
-
Kanname ühele joonisele interpoleerimisel saadud polünoomi graafiku,
andmetabeli punktid ning punkte ühendava murdjoone.
-
In[7]:= Show[g2, p, j]
-
-
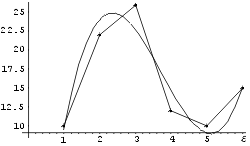
2.3. Numbriline interpoleerimine
-
Interpolation[andmed] Polünomiaalne
interpoleerimine. Lähendfunktsiooni analüütilist kuju ei
leita, selle asemel koostatakse nn. InterpolatingFunction'i objekti,
mille abil saab arvutada interpolatsioonipolünoomi väärtusi.
Andmed esitatakse kujul
-
{{ x1 , f(x1)
},
{
x2
,
f(x2)
},...,{
xn
,
f(xn)
}}
või kujul
-
{ f(x1) , f(x2)
,
..., f(xn) } , kui x1
= 1, x2 = 2, ... xn = n.
-
Kui on teada funktsiooni tuletiste väärtused punktides xi
, siis võib funktsiooni väärtuse f(xi)
asendada loendiga
-
{ f(xi) , f'(xi)
,
f''(xi)
,
...}
-
Mitme muutuja funktsiooni interpoleerimisel kirjutatakse punkti Pi
= (xi, yi, ...) koordinaadid ja punktile
vastav funktsiooni väärtus f(Pi) ühte
loendisse:
-
{{ x1 , y1 ,...,
f(P1)
},
{
x2
,
y2
,...,
f(P2)
},...,{
xn
,
yn
,...,
f(Pi)
}}
-
Tuletiste kasutamisel asendatakse funktsiooni väärtus f(Pi)
järgmise loendiga:
-
{ f(Pi) , {
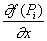 ,
,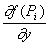 ,...,
,...,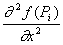 ,
,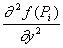 ,
...}}.
,
...}}.
-
Lähendpolünoomi astet saab muuta parameetriga InterpolationOrder->aste.
Vaikimisi on aste 3, seega lähendatakse andmeid kuupparabooliga.
Interpolation
annab
lähendfunktsiooni numbriliselt, mitte analüütiliselt. Tulemus
väljastatakse kujul:
-
InterpolatingFunction[{a, b}, <>]
-
Siin {a, b} näitab piirkonda, milles funktsioon on interpoleeritud.
Lähendpolünoomi määravate arvuloendite asemel trükitakse
kolmnurksulud <>. Nii esitatud funktsiooni väärtuse
arvutamiseks kohal x = x0 kasutatakse süntaksit
-
InterpolatingFunction[{a, b}, <>][x0]
-
-
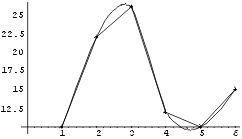
Näide 3. Leiame lähendi esimeses näites toodud andmetabelile.
-
In[8]:= poly3 = Interpolation[{10,22,26,12,10,15}]
-
Out[8]= InterpolatingFunction[{1,
6}, <>]
-
-
Arvutame interpolatsioonipolünoomi väärtuse punktis x
= 2,34:
-
In[9]:= poly3[2.34]
-
Out[9]= 24.7588
-
-
Et võrrelda saadud lähendfunktsiooni tegelike andmetega, joonestame
tema graafiku ja märgime samale joonisele ka andmetabeli punktid.
Seejuures kasutame esimese näite arvutustulemusi.
-
-
In[10]:= g3 = Plot[ poly3[x], {x,1,6},
DisplayFunction->Identity];
-
Show[g3, p, j, DisplayFunction->$DisplayFunction]
-
-
-
§3. ASTMEREAD
3.1. Summad ja korrutised
Sum[ f(i), {i,
imax}]
Arvutab
summa 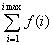 .
.
Sum[ f(i), {i,
imin,
imax}]
Arvutab
summa 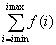 .
.
Sum[ f(i), {i,
imin,
imax,
di}]
Arvatab
summa, muutes summeerimisindeksit sammuga di.
Sum[ f(i, j), {i,
imax},
{j,
jmax}]
Arvutab
kahekordse summa 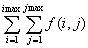 .
Summeerimisindekseid võib olla rohkem kui kaks. Iga indeksi korral
võib määrangu {i, imax}
asemel
kasutada määrangut {i,
imin,
imax}
või {i,
imin,
imax,
di}.
.
Summeerimisindekseid võib olla rohkem kui kaks. Iga indeksi korral
võib määrangu {i, imax}
asemel
kasutada määrangut {i,
imin,
imax}
või {i,
imin,
imax,
di}.
-
Näide 1. Arvutame saja esimese naturaalarvu ruutude summa,
s. o. summa
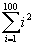 .
.
-
In[1]:= Sum[i^2, {i,100}]
-
Out[1]= 338350
-
NSum[ f(i), {i,
imax}]
Arvutab
numbriliselt summa
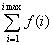 .
Indeksi(te) väärtuste määramisel saab kasutada kõiki
käsu Sum jaoks toodud variante. Numbrilise summeerimise korral
võib summeerimisraja väärtuseks olla ka lõpmatus.
.
Indeksi(te) väärtuste määramisel saab kasutada kõiki
käsu Sum jaoks toodud variante. Numbrilise summeerimise korral
võib summeerimisraja väärtuseks olla ka lõpmatus.
-
Näide 2. Leiame rea
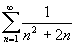 summa.
summa.
-
In[2]:= NSum[1/(n^2+2n), {n,Infinity}]
-
Out[2]= 0.75
-
Näide 3. Leiame rea
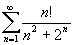 summa.
summa.
-
In[3]:= NSum[ n!/(n^2+2^n),
{n,Infinity}]
-
Out[3]= ComplexInfinity
-
Vastus tähendab, et antud rida hajub.
Product[ f(i), {i,
imax}]
Arvutab
korrutise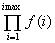 . Indeksi(te)
väärtuste määramisel saab kasutada kõiki käsu
Sum jaoks toodud variante.
. Indeksi(te)
väärtuste määramisel saab kasutada kõiki käsu
Sum jaoks toodud variante.
-
Näide 4. Arvutame kõigi 20-st väiksemate paaritute
naturaalarvude korrutise.
-
In[4]:= Product[i,{i,1,20,2}]
-
Out[4]= 654729075
-
Antud juhul võiks sama korrutist arvutada ka poolfaktoriaali abil.
-
In[5]:= (20-1)!!
-
Out[5]= 654729075
-
NProduct[ f(i), {i,
imax}]
Arvutab
numbriliselt korrutise
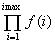 .
Indeksi(te) väärtuste määramisel saab kasutada kõiki
käsu Sum jaoks toodud variante.
.
Indeksi(te) väärtuste määramisel saab kasutada kõiki
käsu Sum jaoks toodud variante.
3.2. Funktsiooni arendamine astmereaks
Astmeridade teooria põhjalik käsitlus on toodud õpikus
[6].
-
Series[f(x), {x,
x0,
n}]
Arendab
funktsiooni
f(x) astmereaks punktis x0.
Reaksarendus leitakse kuni astmeni (x - x0)n.
-
Series[f(x; y), {x,
x0,
xn},{y,
y0,
yn}]
Arendab
kahe muutuja funktsiooni f(x;
y) astmereaks; esmalt
muutuja
y järgi, siis muutuja
x järgi.
-
Astmereaks arendatud funktsioone käsitleb Mathematica kui teatavat
erilist tüüpi objekte, mida nimetatakse SeriesData objektideks.
SeriesData
objekt väljastatakse kujul
-
2 3
n
-
a0 + a1(x-x0) + a2(x-x0) + a3(x-x0) +...+ O[x-x0] ,
-
kus O[x-x0]^n on rea jääkliige. SeriesData objektidega
saab teha aritmeetilisi tehteid, neist saab leida tuletist ja integraali.
Tulemuseks saame seejuures ikka SeriesData objekti. SeriesData
objektist ei saa joonestada graafikut ega arvutada tema väärtust
konkreetse x korral. Et seda teha, tuleb reaksarendus enne teisendada
tavaliseks avaldiseks, nagu näidatakse järgmises punktis.
-
Näide 5. Leiame funktsiooni y = sin x reaksarenduse
punkti x = 1 ümbruses kuni astmeni (x - 1)4.
-
-
In[6]:= Series[Sin[x],{x,1,4}]
-
Out[6]=
2
-
Sin[1] (-1 + x)
-
Sin[1] + Cos[1] (-1 + x)
- ---------------- -
-
2
-
-
3
4
-
Cos[1] (-1 + x)
Sin[1] (-1 + x)
5
-
---------------- + ----------------
+ O[-1 + x]
-
6
24
-
InverseSeries[rida, x]
Leiab
reaksarenduse käsuga Series astmereaks arendatud funktsiooni
pöördfunktsioonile. Korraldus InverseSeries võib
osutuda kasulikuks pöördfunktsiooni leidmisel. On olemas küllalt
palju funktsioone, mille pöördfunktsiooni ei ole võimalik
analüütilisel kujul avaldada; sel juhul on oluline leida vähemalt
pöördfunktsiooni reaksarendus.
-
-
Näide 6. Leiame reaksarenduse funktsioonile f(x)
= ex - 1 punkti x = 0 ümbruses kuni astmeni
x3.
Saadud tulemust kasutades arendame astmereaks funktsiooni
f(x)
pöördfunktsiooni g(x) = ln(x + 1).
-
-
In[7]:= f = Series[E^x-1, {x,0,5}]
-
Out[7]=
2 3 4 5
-
x x x x
6
-
x + -- + -- + -- + --- +
O[x]
-
2 6 24 120
-
-
In[8]:= g = InverseSeries[f, x]
-
Out[8]=
2 3 4 5
-
x x x x
6
-
x - -- + -- - -- + -- +
O[x]
-
2 3 4 5
3.3. Reaksarenduse teisendamine funktsiooniks
Nagu eelmises punktis nimetatud, on SeriesData objektide kasutamisel
mõned piirangud. Neist vabanemiseks tuleb minna üle tavalisele
astmefunktsioonile.
-
Normal[avaldis] Teisendab SeriesData
objekti tavaliseks avaldiseks, jättes ära kõrgemat järku
väikese O[x-x0]^n.
-
-
Näide 7. Teisendame viiendas näites saadud siinuse astmerea
astmefunktsiooniks.
-
In[9]:= Normal[%6]
-
Out[9]=
3
-
(-1 + x) Cos[1]
-
(-1 + x) Cos[1] - ----------------
+ Sin[1] -
-
6
-
-
2
4
-
(-1 + x) Sin[1]
(-1 + x) Sin[1]
-
---------------- + ----------------
-
2
24
-
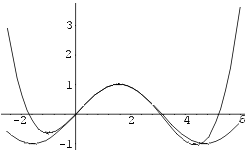
Kanname ühele joonisele funktsiooni y = sin x graafiku
ja tema reaksarendusele vastava astmefunktsiooni graafiku.
-
In[10]:= Plot[ {%9,Sin[x]}, {x,-2.5,6}]
-
-
-
§4. MAATRIKSARVUTUS
Maatriksite ja determinantide kohta leiab lugeja abimaterjali raamatust
[4].
4.1. Ühikmaatriks ja diagonaalmaatriks
Arvutuste käigus läheb sageli vaja mingit järku ühikmaatrikist
või diagonaalmaatriksit, kui diagonaalil olevad elemendid on teada.
Selliste maatriksite genereerimiseks on olemas spetsiaalsed käsud.
-
IdentityMatrix[n] Trükib n
järku ühikmaatriksi.
-
Näide 1. Kolmerealine ühikmaatriks:
-
In[1]:= TableForm[ IdentityMatrix[3]
]
-
Out[1]//TableForm=
-
1 0 0
-
0 1 0
-
0 0 1
-
-
DiagonalMatrix[{a1, a2,
..., an}] Annab maatriksi, mille
peadiagonaalil on elemendid a1,
a2,
... , an ja kõik muud elemendid on nullid; s.t.
diagonaalmaatriksi.
-
Näide 2. Maatriks, mille peadiagonaalil on arvud 2, 3 ja 1
ning muud elemendid on nullid.
-
In[2]:= TableForm[ DiagonalMatrix[{2,-3,1}]
]
-
Out[2]//TableForm=
-
2 0 0
-
0 -3 0
-
0 0 1
4.2. Determinandid ja miinorid
-
Det[M] Arvutab ruutmaatriksi M
determinandi.
-
-
Näide 3. Leiame maatriksi
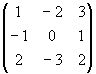 determinandi.
determinandi.
-
In[3]:= {{-2,3,4}, {1,-3,2}, {-1,-4,3}}
-
Out[3]= {{-2, 3, 4}, {1, -3, 2},
{-1, -4, 3}}
-
In[4]:= Det[%3]
-
Out[4]= -41
-
-
Minors[M, k] Arvutab
maatriksi M kõik k-ndat järku miinorid. Teiste
sõnadega, leitakse kõigi k × k alammaatriksite
determinandid.
M ei pea olema ruutmaatriks.
-
Näide 4. Arvutame maatriksi M esimest järku miinorid,
kui
-
M =
 .
.
-
-
In[5]:= M = {{a,b}, {c,d},
{e,f}, {g,h}};
-
In[6]:= Minors[M,1]
-
Out[6]= {{a, b}, {c, d},
{e, f}, {g, h}}
-
-
Kuna esimest järku miinor on maatriksi üksik element, saime tulemuseks
esialgse maatriksi. Teist järku miinoriteks on teist järku determinandid.
-
In[7]:= Minors[M,2]
-
Out[7]= {{-b c + a
d}, {-b e + a f}, {-b g + a h}, {-d e + c f},
-
{-d g + c h}, {-f
g + e h}}
-
-
Kõrgemat järku miinoreid maatriksil M ei ole.
4.2. Maatriksi teisendusi
-
Transpose[M] Vahetab maatriksi M
read ja veerud, s.t. transponeerib maatriksi.
-
Näide 5. Leiame maatriksi
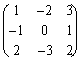 transponeeritud maatriksi.
transponeeritud maatriksi.
-
In[8]:= {{1,-2,3}, {-1,0,1}, {2,-3,2}}
-
Out[8]= {{1, -2, 3}, {-1, 0, 1}, {2, -3,
2}}
-
In[9]:= TableForm[ Transpose[%8] ]
-
Out[9]//TableForm=
-
1 -1 2
-
-2 0 -3
-
3 1 2
-
-
Inverse[M] Leiab ruutmaatriksi M
pöördmaatriksi.
-
-
Näide 6. Leiame eelmise näite maatriksi pöördmaatriksi.
-
In[10]:= TableForm[ Inverse[%8] ]
-
Out[10]//TableForm=
-
3 5 1
-
- -(-) -(-)
-
4 4 2
-
-
1 -1 -1
-
3 1 1
-
- -(-) -(-)
-
4 4 2
-
MatrixPower[M, n] Leiab
ruutmaatriksi
M
n-nda astme, korrutades maatriksit iseendaga
n
korda. Kui
n on negatiivne, leitakse pöördmaatriksi aste.
-
-
Näide 7. Leiame 8. real sisestatud maatriksi kolmanda astme.
-
In[11]:= TableForm[ MatrixPower[%8,3]
]
-
Out[11]//TableForm =
-
34 -39 30
-
0 1 0
-
33 -39 31
-
-
RowReduce[M] Teisendab maatriksi
M
peadiagonaali elemendid ühtedeks ja peadiagonaalist üles ja allapoole
jäävad elemendid nullideks. Sellist operatsiooni nim. mõnikord
ka Gaussi teisenduseks.
-
-
Näide 8. Võtame ühe suvalise maatriksi M ja
teisendame seda..
-
In[12]:= M = {{-26, 5, -9,-158,-144},
-
{ -6, 5, -3, -64, -16},
-
{ 18,-3,-10, -39, 134}};
-
In[13]:= TableForm[RowReduce[M]]
-
Out[13]//TableForm=
-
1 0 0 2 7
-
0 1 0 -5 4
-
0 0 1 9 -2
4.4. Maatriksite (vektorite) korrutamine
-
Dot[A, B]
ehk
A.B
Maatriksite korrutamine. Maatriksid
A ja B peavad olema sobiva
suurusega. Kui tegureid on rohkem kui kaks, siis kirjutatakse A.B.C....
või
Dot[A,B,C,...].
-
Näide 9. Leiame maatriksite korrutise
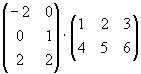 .
.
-
In[14]:= {{-2,0},{0,1},{2,2}};
-
-
In[15]:= {{1,2,3},{4,5,6}};
-
-
In[16]:= TableForm[ %14.%15 ]
-
Out[16]//TableForm=
-
-2 -4 -6
-
4 5 6
-
10 14 18
-
Dot[{a1, a2,
a3},
{b1,
b2,
b3}]
ehk
{a1,
a2,
a3}.{b1,
b2,
b3}
Leiab
vektorite
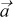 = (a1;
a2;
a3)
ja
= (a1;
a2;
a3)
ja 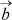 = (b1;
b2;
b3)
skalaarkorrutise.
= (b1;
b2;
b3)
skalaarkorrutise.
-
Cross[{a1, a2,
a3},
{b1,
b2,
b3}]
Arvutab
vektorite
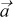 = (a1;
a2;
a3)
ja
= (a1;
a2;
a3)
ja 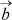 = (b1;
b2;
b3)
vektorkorrutise. NB! Mathematica versioonis 3.0 kuulub see käsk
tuuma funktsioonide hulka ja teda saab kasutada ilma pikema eeltööta.
Versiooni 2.2 (ja teiste madalamate versioonide) korral tuleb aga enne
mällu lugeda
package LinearAlgebra`CrossProduct`.
= (b1;
b2;
b3)
vektorkorrutise. NB! Mathematica versioonis 3.0 kuulub see käsk
tuuma funktsioonide hulka ja teda saab kasutada ilma pikema eeltööta.
Versiooni 2.2 (ja teiste madalamate versioonide) korral tuleb aga enne
mällu lugeda
package LinearAlgebra`CrossProduct`.
-
Näide 10. Arvutame
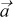 ×
×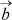 ,
kui
,
kui 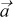 = (2; -3; 7) ja
= (2; -3; 7) ja 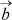 = ( -7; 6; 2). Kui on tarvis, loeme mällu package'i.
= ( -7; 6; 2). Kui on tarvis, loeme mällu package'i.
-
In[17]:= <<LinearAlgebra`CrossProduct`
-
Sümboli ` saab klahvikombinatsiooniga [Alt] + 096. Ja nüüd
sisestame vektorid ja arvutame nende vektorkorrutise.
-
In[18]:= a = {2,-3,7};
-
b = {-7,6,2};
-
In[19]:= Cross[a,b]
-
Out[19]= {-48, -53, -9}
4.5. Maatriksvõrrandid
-
LinearSolve[A, B] Leiab
maatriksi
X, mis on maatriksvõrrandi AX = B
lahendiks.
-
Näide 11. Lahendame maatriksvõrrandi AX = B,
kui A =
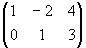 ja B =
ja B = 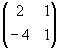 .
.
-
In[20]:= A = {{1,-2,4}, {0,1,3}};
-
B = {{2,1}, {-4,1}};
-
In[21]:= TableForm[ LinearSolve[A,B]
]
-
Out[21]//TableForm=
-
-6 3
-
-4 1
-
0 0
Eelmine
peatükk
Järgmine
peatükk
Sisukord
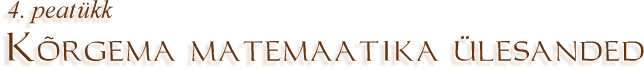








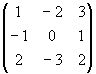 determinandi.
determinandi. .
.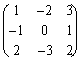 transponeeritud maatriksi.
transponeeritud maatriksi. .
.