
Käesolevas peatükis lahendatakse ülesandeid nii keskkooli
kui ka kõrgema matemaatika vallast. Mathematical on spetsiaalsed
käsud paljude tüüpiliste probleemide lahendamiseks. Seetõttu
on peatükk üles ehitatud nii, et kõigepealt tutvustakse
vastava käsu süntaksit ja seejärel tuuakse näide selle
käsu kasutamisest.
§1. AVALDISTE ALGEBRALINE TEISENDAMINE
1.1. Sulgude avamine ja teguriteks lahutamine
Expand[avaldis] Avab sulud korrutistes
ja astmetes. Astendaja peab olema positiivne täisarv.
-
Näide 1. Korrutame lahti avaldise (2 + a)4.
-
In[1]:= Expand[(2+a)^4]
-
Out[1]=
2 3 4
-
16 + 32 a + 24 a + 8 a +
a
Korraldusel Expand on mõned teisendid, mis lihtsustavad
tööd murruliste avaldistega. Tuleb arvestada, et ka negatiivset
astendajat vaadeldakse murruna.
-
ExpandNumerator[avaldis] Avab sulud
ainult murru lugejas.
-
ExpandDenominator[avaldis] Avab
sulud ainult murru nimetajas.
-
ExpandAll[avaldis] Avab kõikvõimalikud
sulud.
-
Näide 2. Toodud käskude erinevuse näitamiseks teisendame
murdu
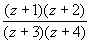 .
.
-
In[2]:= Expand[(z+1)(z+2)/((z+3)(z+4))]
-
Out[2]=
2
-
2
3 z
z
-
-------------- + --------------
+ --------------
-
(3 + z)(4 + z)
(3 + z)(4 + z) (3 + z)(4 + z)
-
-
In[3]:= ExpandNumerator[(z+1)(z+2)/((z+3)(z+4))]
-
Out[3]=
2
-
2 + 3 z + z
-
---------------
-
(3 + z) (4 + z)
-
-
In[4]:= ExpandDenominator[(z+1)(z+2)/((z+3)(z+4))]
-
Out[4]= (1 + z) (2 + z)
-
---------------
-
2
-
12 + 7 z + z
-
-
In[5]:= ExpandAll[(z+1)(z+2)/((z+3)(z+4))]
-
Out[5]=
2
-
2
3 z
z
-
------------- + -------------
+ -------------
-
2
2
2
-
12 + 7 z + z
12 + 7 z + z 12 + 7 z + z
Expand[avaldis,muutujad]
Sellise
süntaksi korral avatakse ainult need sulud, mis sisaldavad avaldise
järel loetletud muutujaid.
-
Näide 3. Olgu meil avaldis (p +
a
)(x – 4)(x + 3) , kus p + a
on mingi konstant, mida oleks mõtet koos hoida. Seega tuleb avada
ainult muutujat x sisaldavad sulud.
-
In[6]:= Expand[ (Pi+alfa) (x-4) (x+3),
x]
-
Out[6]=
2
-
-12 (alfa + Pi) - (alfa
+ Pi) x + (alfa + Pi) x
Korraldus Expand töötab ainult täisarvulise astendaja
korral. Murdarvulise astendajaga astendamiseks kasutatakse käsku PowerExpand.
PowerExpand[avaldis] Korrutise,
jagatise ja astme astendamine suvalise astendajaga. Näteks avaldis
(ab)1/3 teisendatakse kujule a1/3 b1/3
ja avaldis (a2)1/3 kujule a2/3.
Avaldis (a + b)1/4 aga väljastatakse muutumatult.
Näidet vaata järgmisest punktist.
Factor[poly] Lahutab polünoomi
teguriteks. Polünoomi kordajad võivad olla murrulised, kuid
nad ei tohi olla irratsionaalsed. Expand ja Factor on
teineteise pöördoperatsioonid.
-
Näide 4. Tegurdame polünoomi 2x3 – 3x2
+ 8x – 12.
-
In[7]:= Factor[ 2x^3 - 3x^2 + 8x - 12 ]
-
Out[7]=
2
-
(-3 + 2 x) (4 + x )
Toodud näitest on näha, et Factor tegurdab ainult reaalsete
nullkohtadega polünoome. Kui soovime saada kompleksarvudega tegureid,
tuleks kasutada süntaksit Factor[poly,
GaussianIntegers->True]
Siin GaussianIntegers on parameeter
ja True sellele parameetrile omistatud väärtus. Vaikimisi
on parameetri GaussianIntegers
väärtus False.
Käskudel Factor ja Expand on veel teisigi parameetreid,
aga neid me siinkohal ei vaatle.
-
Näide 5. Tegurdame uuesti eelmises näites antud polünoomi.
-
In[8]:= Factor[ 2x^3-3x^2+8x-12,
GaussianIntegers->True]
-
Out[8]= (-2 I + x) (2 I + x) (-3
+ 2 x)
1.2. Ühisele nimetajale viimine ja osamurdudeks lahutamine
-
Together[avaldis] Viib avaldise
ühisele nimetajale ja taandab tulemuse. Uues nimetajas jäetakse
võimaluse korral sulud avamata.
-
Näide 6. Viime ühisele nimetajale avaldise
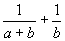 .
.
-
In[9]:= Together[ 1/(a+b) + 1/b ]
-
Out[9]= a + 2 b
-
---------
-
b (a + b)
-
-
Apart[avaldis]
Lahutab avaldise
minimaalsete nimetajatega osamurdudeks. Apart
ja Together
on
teineteise pöördoperatsioonid.
-
Näide 7. Lahutame osamurdudeks avaldise
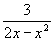 .
.
-
In[10]:= Apart[3/(2-x-x^2)]
-
Out[10]=
1 1
-
-(------) + -----
-
-1 + x
2 + x
1.3. Avaldise lihtsustamine
-
Simplify[avaldis] Lihtsustab avaldise.
Teisendab avaldist, otsides talle kõige lühemat esitust.
-
Näide 8. Lihtsustame avaldise (x – 3)(x + 7)
– x2.
-
In[11]:= Simplify[ (x-3)(x+7) - x^2
]
-
Out11]= -21 + 4 x
-
-
Koos käsuga Simplify saab kasutada parameetrit Trig->
(
True
või False ). Vaikimisi kehtiva väärtuse
True korral kasutatakse lihtsustamisel trigonomeetrilisi samasusi.
Väärtuse False
korral trigonomeetrilisi samasusi ei
kasutata.
-
Näide 9. Lihtsustame avaldise
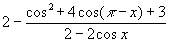 .
.
-
In[12]:= Simplify[2 - (Cos[x]^2 +
4Cos[Pi-x] + 3)/(2 - 2Cos[x])]
-
Out[12]= x 2
-
Cos[-]
-
2
-
Tulemus on esitatud nurga
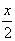 abil. Kui me mingil põhjusel ei soovi poolnurgale üle minna,
tuleks keelata trigonomeetriliste samasuste kasutamine. Siis antakse vastus
nurga x funktsioonina.
abil. Kui me mingil põhjusel ei soovi poolnurgale üle minna,
tuleks keelata trigonomeetriliste samasuste kasutamine. Siis antakse vastus
nurga x funktsioonina.
-
In[13]:= Simplify[2 - (Cos[x]^2 +
4Cos[Pi-x] + 3)/(2 - 2Cos[x]),
-
Trig->False
]
-
Out[13]= 1 + Cos[x]
-
----------
-
2
-
Mõningaid juuravaldisi ( näiteks
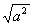 ) ei ole võimalik korraldusega Simplify lihtsustada. Põhjus
seisneb selles, et kuna ei ole teada, kas a on positiivne või
negatiivne, peaks vastuseks olema | a |. Selleks, et taolises avaldises
juuremärgist vabaneda, kasutatakse käsku PowerExpand
. (Vt. p. 2.1.1.)
) ei ole võimalik korraldusega Simplify lihtsustada. Põhjus
seisneb selles, et kuna ei ole teada, kas a on positiivne või
negatiivne, peaks vastuseks olema | a |. Selleks, et taolises avaldises
juuremärgist vabaneda, kasutatakse käsku PowerExpand
. (Vt. p. 2.1.1.)
-
Näide 10. Lihtsustame avaldise
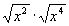 .
.
-
In[14]:= PowerExpand[ Sqrt[x^2] Sqrt[x^4]
]
-
Out[14]= 3
-
x
-
-
Collect[avaldis,x]
Kogub
avaldises kokku liikmed, milles
x-i aste on ühesugune. Korraldust
Collect on sobiv kasutada juhul, kui avaldist vaadeldakse polünoomina
muutujast x.
-
Näide 11. Esitame avaldise (x + xy +1)2
polünoomina muutujast x.
-
In[15]:= Collect[ Expand[(x+x y+1)^2],
x]
-
Out[15]=
2 2
-
1 + x (2 + 2 y) + x (1 +
2 y + y )
-
-
Collect[avaldis,{x1,x2,...}]
Kogub
avaldises kokku liikmed, milles x1 , x2
,
… astmed on ühesugused.
-
§2. VÕRRANDITE
JA VÕRRANDISÜSTEEMIDE LAHENDAMINE
2.1. Algebralised võrrandid
Solve[ p(x) == q(x),
x]
Püüab
lahendada võrrandit p(x) = q(x)
muutuja
x suhtes. Käsuga Solve
saab lahendada põhiliselt
algebralisi võrrandeid. Avaldised
p(x) ja q(x)
võivad muutuja x suhtes sisaldada algebralisi operatsioone,
astendamist ja/või juurimist. Võrrand võib näiteks
sisaldada liikmeid x, x2,
x3y, 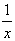 ,
, 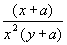 ,
, 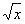 ,
(x + y)0,4, kuid ei tohi sisaldada liikmeid sin
x,
xx,
x
+ ex . Kui selliseid liikmeid esineb, siis tuleb võrrandit
lahendada nagu transtsendentset võrrandit, vt. p. 2.4.3. Lihtsamaid
eksponent- ja logaritmvõrrandeid on Solve-käsuga siiski võimalik
lahendada. (Näiteks 32x = 27.)
,
(x + y)0,4, kuid ei tohi sisaldada liikmeid sin
x,
xx,
x
+ ex . Kui selliseid liikmeid esineb, siis tuleb võrrandit
lahendada nagu transtsendentset võrrandit, vt. p. 2.4.3. Lihtsamaid
eksponent- ja logaritmvõrrandeid on Solve-käsuga siiski võimalik
lahendada. (Näiteks 32x = 27.)
-
Näide 1. Lahendame ruutvõrrandi x2
– 5x – 14 = 0.
-
In[1]:= Solve[ x^2-5x-14==0, x]
-
Out[1]= {{x -> -2}, {x -> 7}}
-
Võrrandi lahenditeks on arvud x = – 2 ja x = 7.
-
-
Nagu näha, esitatakse lahendid loendina, kus on kirjas ka otsitava
tähis. Kui võrrandil on kordseid lahendeid, kirjutatakse igaüks
neist väljundisse vastav arv kordi. Muutuja x märkimine
ei ole käsu Solve korral tingimata vajalik. Seega oleks viimase näites
võinud sisestada rea Solve[ x^2-5x-14==0 ] . Juhul kui
võrrandis on muutujaid rohkem kui üks, oleks siiski soovitav
lisada, millise suhtes neist tuleb võrrandit lahendada. Solve
leiab
ka võrrandi imaginaarsed lahendid.
-
Näide 2. Lahendame murdvõrrandi
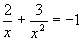 .
.
-
In[2]:= Solve[ 2/x + 3/x^2 == -1,
x]
-
Out[2]=
-2 - 2 I Sqrt[2] -2 + 2
I Sqrt[2]
-
{{x -> ----------------},
{x -> ----------------}}
-
2
2
-
Leitud lahendit saab lihtsustada käsu Simplify abil.
-
In[3]:= Simplify[%2]
-
Out[3]= {{x -> -1 - I Sqrt[2]}, {x -> -1
+ I Sqrt[2]}}
-
Võrrandil on kaks imaginaarset lahendit: x = – 1 – i
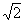 ja x = – 1 + i
ja x = – 1 + i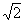 .
.
NSolve[ p(x) == q(x),
x]
Algebralise
võrrandi p(x) = q(x) numbriline lahendamine.
Võrrandi lahend(id) esitatakse kümnendmurruna. Numbrilist lahendamist
on mõtet kasutada kui:
1) Täpset lahendit esitav avaldis on keerukas ja ebaülevaatlik.
2) Mõned võrrandid, mille puhul käsk Solve ei
suuda lahendit leida, on NSolve’le täiesti
jõukohased.
-
Näide 3. Lahendame võrrandi
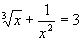 .
(Käsk Solve selle võrrandi lahendeid ei leia.)
.
(Käsk Solve selle võrrandi lahendeid ei leia.)
-
In[4]:= NSolve[ x^(1/3) + 1/x^2 ==
3, x]
-
Out[4]= {{x -> 0.687202}, {x -> 26.9629}}
-
Võrrandil on kaks lahendit: x »
0,687202 ja x » 26,9629.
2.2. Võrrandisüsteemid
-
Solve[{võr1,võr2},{x,y}]
Püüab
lahendada kahest võrrandist koosnevat süsteemi muutujate x
ja y suhtes. Võrrandid peavad olema algebralised, nad ei
tohi sisaldada transtsendentseid funktsioone. Võrrandeid võib
süsteemis olla rohkem kui kaks.
-
Näide 4. Lahendame kolmest võrrandist koosneva süsteemi
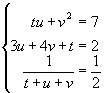 .
.
-
In[5]:= Solve[{ t*u+v^2==7,
-
3 u+4 v+t==2,
-
1/(t+u+v)==1/2}, {t,u,v} ]
-
Out[5]= {{t -> 1, u -> 3, v -> -2},
-
{t -> 9, u -> -21,
v -> 14}}
-
Võrrandil on kaks lahendit:
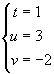 ja
ja 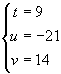 .
.
-
Vaadeldud näites oli võrrandisüsteem esitatud loendina.
Teine võimalus on ühendada võrrandid süsteemiks
loogilise ja-sümboli abil, milleks on &&.
-
-
Solve[{võr1,võr2},
x,
y]
Püüab
lahendada võrrandisüsteemi muutuja
x suhtes, elimineerides
seejuures muutuja y.
-
Näide 5. Lahendame võrrandisüsteemi
-
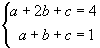 muutuja
a
suhtes ja elimineerime muutuja b. Samaaegselt lihtsustame tulemust.
muutuja
a
suhtes ja elimineerime muutuja b. Samaaegselt lihtsustame tulemust.
-
In[6]:= Simplify[ Solve[ {a+2b+c==4,
a+b+c==1} ,a, b] ]
-
Out[6]= {{a -> -2 - c}}
-
Saime, et a esitub muutuja c kaudu järgmiselt: a
= – 2 – c.
-
-
Eliminate[{võr1,võr2},
x]
Elimineerib
võrrandisüsteemist muutuja x. Kui tulemuses on rohkem
kui üks võrrand, siis ühendatakse võrrandid loogilise
ja-sümboli &&
abil.
-
Näide 6. Elimineerime võrrandisüsteemist
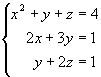 muutuja
z.
muutuja
z.
-
In[7]:= Eliminate[ {x^2+y+z==4, 2x+3y==1,
y+2z==1}, z]
-
Out[7]= 2
-
-x + 3 x == 10 &&
3 y == 1 - 2 x
-
Olles elimineerinud esialgsest võrrandisüsteemist muutuja
z,
saame kahest võrrandist koosneva süsteemi
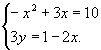
2.3. Transtsendentsed võrrandid
FindRoot[ f(x) == g(x),
{x,x0}] Otsib
võrrandi f(x) = g(x) ligikaudset lahendit
Newtoni meetodil. Siin f(x) ja g(x) võivad
olla suvalised funktsioonid, x on muutuja, mille suhtes võrrandit
lahendatakse, x0 on aga lahendi alglähend.
-
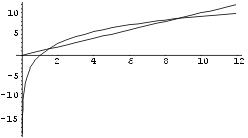
Näide 7. Lahendame võrrandi 4 ln x = x.
Alglähendi määramiseks joonestame kõigepealt funktsioonide
y
= 4 ln x ja y = x graafikud mingis mõistlikult
valitud piirkonnas. Graafikute lõikepunkti
x-koordinaadi
võib võtta esialgseks lähendiks
x0.
-
In[8]:= Plot[ {4 Log[x],x},
{x,0.01,12} ]
-
-
-
-
In[9]:= FindRoot[4 Log[x]==x,
{x,2}]
-
Out[9]= {x -> 1.42961}
-
In[10]:= FindRoot[4 Log[x]==x,
{x,8}]
-
Out[10]= {x -> 8.61317}
FindRoot[f(x) == g(x),
{x,{x0,x1}}]
Otsib
võrrandi f(x) = g(x) ligikaudset lahendit
kõõlude meetodil, x0 ja x1
on lahendi alglähendid.
FindRoot[f(x) == g(x),
{x,{x0,xmin,xmax}}]
Alglähendiks
võetakse x0. Lahendi otsimisel peatutakse, kui
x
väärtus satub väljapoole piirkonnast [xmin
; xmax].
FindRoot[{võr1, võr2},
{x,
x0},{y,
y0}]
Otsib
kahest võrrandist koosneva võrrandisüsteemi ligikaudset
lahendit, x0 ja y0 on vastavalt tundmatute
x
ja y alglähendid. Võrrandeid ja tundmatuid võib
süsteemis olla ka rohkem. Peab ütlema, et kahe või enama
muutuja korral võib alglähendite leidmine olla küllalt
tülikas.
-
Näide 8. Lahendame võrrandisüsteemi
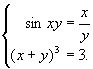
-
Ei ole olemas lihtsaid algoritme sellisele võrrandisüsteemile
alglähendite leidmiseks, veel enam, on raske hinnata isegi lahendite
arvu. Millised alglähendid valida ja mitu lahendit leida, see sõltub
põhiliselt tundmatute x ja y sisulisest tähendusest.
Samuti on ilmne, et näiteks y0 = 0 antud juhul lähendiks
ei sobi.
-
Alglähendite x0 = 1 ja y0 = 1
korral saame järgmise tulemuse:
-
In[11]:= FindRoot[ {Sin[x y]==x/y,(y+x)^3==3},
-
{x,1}, {y,1}]
-
Out[11]= {x -> 0.426391, y -> 1.01586}
-
Alglähendite x0 = 10 ja y0 = 10
korral saame teistsuguse lahendi.
-
In[12]:= FindRoot[{Sin[x y]==x/y,(y+x)^3==3},
-
{x,10},{y,10}]
-
Out[12]= {x -> -96.1433, y -> 97.5855}
-
§3. MIINIMUMIDE
JA MAKSIMUMIDE LEIDMINE
3.1. Lokaalne miimimum ja maksimum
FindMinimum[f(x),{x,x0}]
Otsib
funktsiooni f(x) lokaalset miinimumi. Arv
x0
on alglähend.
Vastus antakse kujul {f(a),{x
->
a}},
kus f(a) on funktsiooni
f(x) miinimumväärtus
ja a on miinimumkoht.
-
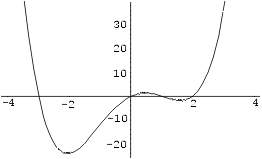
Näide 1. Leiame funktsiooni y = x4
– 7x2 + 6x miinimumid. Esmalt joonestame funktsiooni
-
y = y(x) graafiku, et teha kindlaks, kas funktsioonil
üldse on miinimumi ja kui on, siis millise võiks valida alglähendi.
-
In[1]:= Plot[x^4 - 7x^2 + 6x, {x,-4,4}]
-
-
-
-
In[2]:= FindMinimum[x^4 - 7x^2 +
6x, {x,-2}]
-
Out[2]= {-24.0573, {x -> -2.05655}}
-
Teise lokaalse miinimumi leidmiseks peame valima teistsuguse alglähendi.
-
In[3]:= FindMinimum[x^4 - 7x^2 +
6x, {x,2}]
-
Out[3]= {-1.76641, {x -> 1.60096}}
FindMinimum[f(x),{x,{x0,x1}}]
Otsib
funktsiooni f(x) lokaalset miinimumi, x0
ja x1 on alglähendid. Sellist süntaksit tuleb
kasutada siis, kui funktsiooni f(x) tuletist ei saa analüütiliselt
leida.
FindMinimum[f(x),{x,x0,xmin,xmax}]
Alglähendiks
võetakse x0. Miinimumi otsimine lõpetatakse,
kui x väärtus satub väljapoole piirkonnast [xmin
; xmax].
FindMinimum[f(x; y; ...),{x,x0},{y,y0},…]
Otsib
mitme muutuja funktsiooni lokaalset miinimumi. x0 ja
y0
on vastavalt muutujate x ja y alglähendid.
Mathematica võtmesõnade hulgas puudub väljend
FindMaximum. Seepärast tuleb funktsiooni f(x) lokaalse
maksimumi leidmiseks kasutada korraldust FindMinimum[ – f(x)
,{x,x0}]
.
Vastuse saame kujul { – f(b) ,{x
-> b}}. See tähendab, et b on küll
funktsiooni f(x) maksimumkoht, kuid funktsiooni väärtus
sellel kohal on f(b). (Esimene arv vastuses tuleb võtta
vastupidise märgiga.)
-
Näide 2. Leiame eelmises näites vaadeldud funktsiooni
y
= x4 – 7x2 + 6x lokaalse maksimumi.
-
In[4]:= FindMinimum[-(x^4 - 7x^2
+ 6x), {x,1}]
-
Out[4]= {-1.32369, {x -> 0.455589}}
-
Seega, funktsioonil f(x) on maksimum punktis (0,45589; 1,32369).
3.2. Lineaarne planeerimine
LinearProgramming[C, A ,B
]
Korraldust
kasutatakse järgmise lineaarse planeerimise ülesande lahendamiseks:
Leida sihifunktsiooni
c1x1 + c2x2
+ . . . +cnxn miinimum nii, et x1,
x2,
. . .
xn rahuldaksid tingimusi:
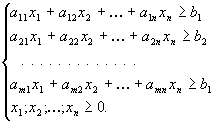
Esitame ülesande maatrikskujul. Selleks võtame kasutusele
tähistused:
Sihifunktsiooni kordajate vektor (c1; c2;
. . . cn) = C.
Võrratuste süsteemi kordajate maatriks  = A.
= A.
Vabaliikmete veeruvektor  = B ja tundmatute veeruvektor
= B ja tundmatute veeruvektor  = X.
= X.
Ülesanne esitub kujul 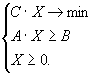
Korraldus LinearProgramming[C,A,B]
leiab
vektori X, mis on selle ülesande lahendiks. Vektorid
B
ja C ning maatriks A peavad olema numbrilised.
Näide 3. Lahendame lineaarse planeerimise ülesande
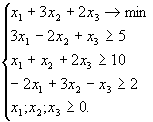
-
In[5]:= A = {{3,-2,1}, {1,1,2}, {-2,3,-1}};
-
B = {5,10,2};
-
C = {1,3,2};
-
In[6]:= LinearProgramming[C, A, B]
-
Out[6]= 7 7
3
-
{-, -, -}
-
2 2 2
-
Sihifunktsiooni väärtuse sellel kohal saab leida kui vektorite
C
ja X skalaarkorrutise. Meenutame, et skalaarkorrutise arvumiseks
võib tehtemärgina kasutada punkti.
-
In[7]:= C.%6
-
Out[7]= 17
3.3. Globaalne miimum ja maksimum
ConstrainedMin[f(x; y; ...),
võrratused,
{x,y,...}]
Leiab
funktsiooni f(x; y; ...) globaalse miinimumi võrratustega
määratud piirkonnas. Nii funktsioon
f(x;
y;
...) kui ka piirkonda määravad võrratused peavad olema
muutujate x, y, … suhtes lineaarsed. Muutujad
x,
y,
… loetakse seejuures mittenegatiivseteks. Võrratused ei tohi sisaldada
kompleksarve ega teisi parameetreid peale muutujate loetelus
{x,y,...}
nimetatute.
Vastus antakse kujul {fmin ,{x
->
xmin
,
y
-> ymin
,…}}. Siin fmin
on funktsiooni miinimumväärtus ja
xmin , ymin
,
… määravad punkti, kus funktsioon selle väärtuse saavutab.
Käsku ConstrainedMin kasutatakse sageli lineaarse planeerimise
ülesannete lahendamisel.
-
Näide 4. Lahendame käsu CostrainedMin abil eelmises
näites antud ülesande
-
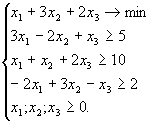
-
-
In[8]:= ConstrainedMin[ x1 + 3 x2
+ 2 x3,
-
{3 x1
- 2 x2 + x3 >= 5,
-
x1 + x2 + 2 x3 >= 10,
-
-2 x1 + 3 x2 - x3 >= 2},
-
{x1, x2, x3}]
-
Out[8]=
7 7
3
-
{17, {x1 -> -, x2 -> -, x3 ->
-}}
-
2 2
2
-
ConstrainedMax[f(x; y; ...),
võrratused,
{x,y,...}]
Leiab
funktsiooni f(x; y;…) globaalse maksimumi võrratustega
määratud piirkonnas. Korraldus ConstrainedMax
töötab
analoogiliselt korraldusega ConstrainedMin.
-
§4. PIIRVÄÄRTUSE,
TULETISE JA INTEGRAALI LEIDMINE
4.1. Piirväärtus
-
Limit[f(x), x->x0]
Leiab
funktsiooni
f(x) piirväärtuse x lähenemisel
x0-le.
-
Näide 1. Leiame piirväärtuse
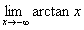
-
In[1]:= Limit[ ArcTan[x], x->-Infinity
]
-
Out[1]= -Pi
-
---
-
2
-
Seda, kummalt poolt x läheneb x0-le, saab
määrata parameetriga Direction.
-
Direction->1 x läheneb x0-le
vasakult.
-
Direction->-1 x läheneb x0-le
paremalt.
-
Direction->Automatic See on vaikimisi kehtiv väärtus,
mille korral lähenetakse x0-le alati paremalt, välja
arvatud protsessi x ®¥ korral.
-
Näide 2. Arvutame piirväärtuse
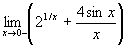 .
(x läheneb 0-le vasakult.)
.
(x läheneb 0-le vasakult.)
-
In[2]:= Limit[ 2^(1/x) + 4 Sin[x]/x,
-
x->0, Direction->1]
-
Out[2]= 4
4.2. Tuletis
Käesolevas punktis vaatleme funktsiooni tuletise, osatuletise ja diferentsiaali
leidmist. Tuletise ja temaga seonduvate mõistete põhjalik
selgitus on toodud õpikutes [5] ja [6].
-
D[ f, x] Leiab
funktsiooni f tuletise x järgi. Kui f on mitme
muutuja funktsioon, siis leitakse osatuletis.
-
Näide 3. Leiame funktsiooni f(x) =
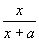 tuletise x-i järgi.
tuletise x-i järgi.
-
In[3]:= D[x/(x+a), x]
-
Out[3]=
x 1
-
-(--------) + -----
-
2 a + x
-
(a + x)
-
Tulemust on ilmselt võimalik lihtsustada.
-
In[4]:= Simplify[%3]
-
Out[4]= a
-
--------
-
2
-
(a + x)
D[f, {x,n}]
Leiab
funktsiooni
n-nda osatuletise
x järgi.
D[f,x,y,…]
Leiab
funktsiooni f segatuletise muutujate x, y, … järgi.
Dt[f ] Leiab funktsiooni f
täisdiferentsiaali df.
-
Näide 4. Leiame kahe muutuja funktsiooni f(x;
y)
= xy2 täisdiferentsiaali.
-
In[5]:= Dt[ x*y^2 ]
-
Out[5]= 2
-
y Dt[x] + 2 x y Dt[y]
-
Otsitav täisdiferentsiaal df(x; y) = y2
dx
+ 2xy dy.
-
-
Dt[f, x] Leiab
funktsiooni f täistuletise
x järgi eeldusel, et
kõik ülejäänud muutujad sõltuvad
x-ist.
-
Näide 5. Leiame funktsiooni f(x; u) =
x2
+ sin u täistuletise, kui u =
u(x).
-
In[6]:= Dt[x^2 + Sin[u], x]
-
Out[6]= 2 x + Cos[u] Dt[u, x]
-
Otsitav täistuletis
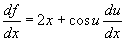 .
.
-
-
Dt[f,{x,n}]
Leiab
funktsiooni f n-ndat järku täistuletise
x-i
järgi.
-
Näide 6. Leiame eelmises näites vaadeldud funktsiooni
teise tuletise x-i järgi.
-
In[7]:= Dt[x^2 + Sin[u], {x,2}]
-
Out[7]=
2
-
2 + Cos[u] Dt[u, {x, 2}]
- Dt[u, x] Sin[u]
-
Otsitav tuletis
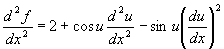 .
.
-
-
Koos käsuga Dt saab kasutada parameetrit Constants->{muutujad},
mis võimaldab ära näidata x-st sõltumatud
muutujad. Vaikimisi loetakse kõiki muutujaid x-i funktsioonideks.
-
Näide 7. Leiame tuletise funktsioonist f(x) =
x2
+ sin u , kui u on konstant.
-
In[8]:= Dt[ x^2+Sin[u]^2, x,Constants->u]
-
Out[8]= 2 x
4.3. Integraal
-
Siin käsitleme määramata ja määratud integraalide
ning kordsete integraalide leidmist. Täiendavat materjali nende teemade
kohta võib leida raamatutest [5] ja [6].
-
Integrate[f(x),x]
Leiab
funktsiooni f(x) määramata integraali
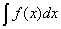 .
.
-
Näide 8. Leiame integraali
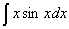 .
.
-
In[9]:= Integrate[x Sin[x], x]
-
Out[9]= -(x Cos[x]) + Sin[x]
-
Saime, et
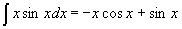 .
Mathematica
ei lisa leitud algfunktsioonile määramata konstanti.
.
Mathematica
ei lisa leitud algfunktsioonile määramata konstanti.
-
Integrate[f(x), {x,x1,x2}]
Leiab
funktsiooni f(x) määratud integraali
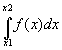 .
.
-
Integrate[f(x; y), {x,x1,x2},
{y,y1,y2}]
Kahekordne
integraal
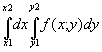 .
Esimesena integreeritakse viimasele kohale kirjutatud muutuja järgi,
mis vastab sisemisele integraalile.
.
Esimesena integreeritakse viimasele kohale kirjutatud muutuja järgi,
mis vastab sisemisele integraalile.
-
Näide 9. Arvutame kahekordse integraali
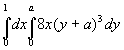 .
.
-
In[10]:= Integrate[8 x (y+a)^3, {x,0,1},
{y,0,a}]
-
Out[10]= 4
-
15 a
-
NIntegrate[f(x), {x,x1,x2}]
Arvutab
numbriliselt funktsiooni f(x) määratud integraali
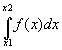 .
Selle käsu abil on võimalik leida integraale ka paljudest sellistest
funktsioonidest, mida analüütilisel kujul integreerida ei ole
võimalik. Korralduse NIntegrate abil saab arvutada ka kordseid
integraale. NIntegrate kontrollib alumise ja ülemise raja
korral, kas funktsioonil ei ole neil kohtadel iseäraseid punkte.
.
Selle käsu abil on võimalik leida integraale ka paljudest sellistest
funktsioonidest, mida analüütilisel kujul integreerida ei ole
võimalik. Korralduse NIntegrate abil saab arvutada ka kordseid
integraale. NIntegrate kontrollib alumise ja ülemise raja
korral, kas funktsioonil ei ole neil kohtadel iseäraseid punkte.
-
NIntegrate[f(x), {x0,x1,…,xn}]
Iseäraste
punktide olemasolu kontrollitakse x väärtuste
x0,
x1,
… xn korral.
-
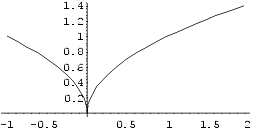
Näide 10. Leiame määratud integraali
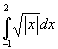 .
Joonestame integraalialuse funktsiooni graafiku integreeritavas piirkonnas.
.
Joonestame integraalialuse funktsiooni graafiku integreeritavas piirkonnas.
-
In[11]:= Plot[ Sqrt[Abs[x]], {x,-1,2},
-
AspectRatio->Automatic]
-
-
-
-
Jooniselt on näha, et punkt x = 0 on funktsiooni iseärane
punkt.
-
In[12]:= NIntegrate[ Sqrt[Abs[x]],
{x,-1,0,2} ]
-
Out[12]= 2.55228
Eelmine
peatükk
Järgmine
peatükk
Sisukord

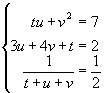 .
.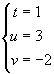 ja
ja 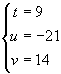 .
.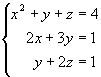 muutuja
z.
muutuja
z.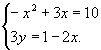

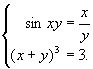

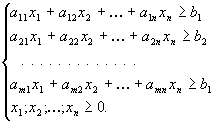
 = A.
= A.
![]() = B ja tundmatute veeruvektor
= B ja tundmatute veeruvektor ![]() = X.
= X.
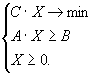
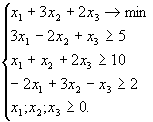
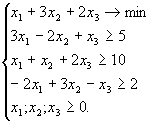
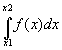 .
.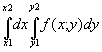 .
Esimesena integreeritakse viimasele kohale kirjutatud muutuja järgi,
mis vastab sisemisele integraalile.
.
Esimesena integreeritakse viimasele kohale kirjutatud muutuja järgi,
mis vastab sisemisele integraalile.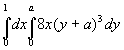 .
.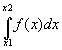 .
Selle käsu abil on võimalik leida integraale ka paljudest sellistest
funktsioonidest, mida analüütilisel kujul integreerida ei ole
võimalik. Korralduse NIntegrate abil saab arvutada ka kordseid
integraale. NIntegrate kontrollib alumise ja ülemise raja
korral, kas funktsioonil ei ole neil kohtadel iseäraseid punkte.
.
Selle käsu abil on võimalik leida integraale ka paljudest sellistest
funktsioonidest, mida analüütilisel kujul integreerida ei ole
võimalik. Korralduse NIntegrate abil saab arvutada ka kordseid
integraale. NIntegrate kontrollib alumise ja ülemise raja
korral, kas funktsioonil ei ole neil kohtadel iseäraseid punkte.