ListPlot[punktid] Joonestab
koordinaatteljestiku ja märgib sinna loetletud punktid. Punktide loetelu
esitatakse kujul
{{x1, y1},{x2,
y2},
}
või kujul
{y1, y2,
}, kui x1 = 1, x2 = 2, jne.
Koos ListPlotiga saab kasutada enamust Plot-käsu
juures loetletud valikuparameetritest. Lisaks on mõistlik kasutada
ühte kahest järgmisest parameetrist:
PlotJoined->True Punktid ühendatakse murdjoonega.
PlotStyle->PointSize[0.03] Määrab punktide
suuruse joonisel. Parameetri sellise väärtuse korral tehakse
punktid piisavalt suured, et neid ekraanil näha oleks.
Hoiatus: sisestades käsu ListPlot ilma parameetriteta,
saame joonise, kus on näha vaid koordinaatteljed.
Näide 12. Olgu meil sagedustabel, kus x omandab väärtusi
1 6.
x
1 2 3
4 5
6
y 15
17 18 17,5 16
25,5
In[15]:=
andmed = {15, 17, 18, 17.5, 16, 15.5}
Out[15]=
{15, 17, 18, 17.5, 16, 15.5}
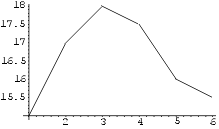
Kui parameetri PlotJoined väärtuseks määrata
True, ühendatakse punktid murdjoonega. Nii saame joonestada sagedustabelile
vastava jaotuspolügooni.
In[16]:=
ListPlot[ andmed, PlotJoined->True]
In[17]:=
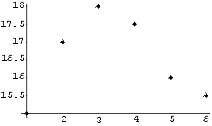
ListPlot[ andmed, PlotStyle->PointSize[0.03]]
§2. KAHE
MUUTUJA FUNKTSOONI GRAAFIKU JOONESTAMINE
2.1. Funktsiooni z = f(x; y) graafik
Plot3D[f(x; y),{x,xmin,xmax},{y,ymin,ymax}]
Joonestab võrrandiga z = f(x; y) määratud
pinna piirkonnas
[ xmin ; xmax] ´
[ ymin ; ymax]. Erinevalt Plot-käsust
ei saa Plot3D-ga joonestada mitut graafikut korraga. Selleks,
et ühel joonisel kujutada kaks või rohkem pinda, tuleb need
pinnad enne eraldi valmis joonestada ja seejärel korralduse Show
abil
ühele joonisele kanda.
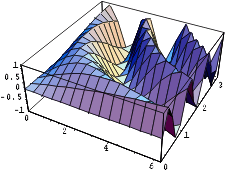
Näide 1. Joonestame pinna, mille võrrand on z
= sin(xy), kui x Î [0; 2p
] ja y Î [0; p
].
In[1]:=
Plot3D[Sin[x*y] ,{x,0,2 Pi},{y,0,Pi}]
Koos käsuga Plot3D saab kasutada ka parameetreid. Mõned
neist on analoogilised vastavate kahemõõtmelise graafika
parameetritega, mõned aga on tarvitusel üksnes ruumigraafika
korral. Parameetrite täielik loetelu on toodud lisas B.
HiddenSurface-> ( True või
False )
Vaikimisi True.
Väärtuse False korral joonestatakse pind sõrestikmudelina.
Kuna värve ei kasutata, toimub joonestamine kiiremini.
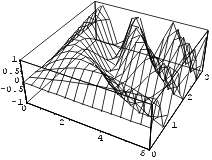
Näide 2. Joonestame uuesti eelpool toodud pinna, andes
parameetrile HiddenSurface väärtuseks False.
In[2]:=
Plot3D[ Sin[x*y] ,{x,0,2 Pi}, {y,0,Pi},
HiddenSurface->False]
AxesLabel->{"x-nimi","y-nimi","z-nimi"}
Vaikimisi None.
Koordinaattelgede juurde nimetuste kirjutamine. Analoogiline parameeter
on olemas ka kahemõõtmelise jooniste jaoks. Ruumijooniste
korral on telgede tähistamine olulisem, sest pinda võib vaadata
suvalise nurga alt ja iga kord ei ole lihtne aru saada, milline on x-telg
ja milline y-telg.
PlotPoints->{nx ,ny
}
Vaikimisi {15,15}.
Määrab, mitu alajaoutuspunkti arvutatakse pinna joonestamiseks
x-
ja y-telje suunas.
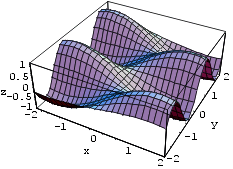
Näide 3. Joonestame võrrandiga z =
sin
x sin 3y määratud pinna, kui x
Î
[ 2; 2] ja y Î [ 2; 2]. Alajaotuspunkte
võtame mõlemas suunas 25. Parameetriga AxesLabel kirjutame
koordinaattelgede juurde tähised.
In[3]:=
Plot3D[ Sin[x] Sin[3y], {x,-2,2}, {y,-2,2},
PlotPoints->{25,25},
AxesLabel->{"x","y","z"}]
ViewPoint->{vpx,vpy,vpz}
Vaikimisi {1.3,-2.4,2} .
Määrab punkti, millest pinda vaadatakse. Vaatepunkti valikut
lihtsustab selektor, mille avab klahvikombinatsioon [Ctrl] + [Shift] +
V või hiireklõps koordinaatteljestikuga nupul  . Selektoril olev kuubik pööratakse liugurite abil sobivasse
asendisse, vajutus nupule Paste kirjutab valitud vaatepunkti käsureale
kursori asukohta.
. Selektoril olev kuubik pööratakse liugurite abil sobivasse
asendisse, vajutus nupule Paste kirjutab valitud vaatepunkti käsureale
kursori asukohta.
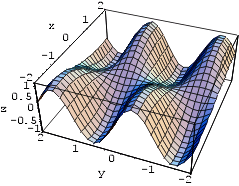
Näide 4. Teeme eelmises näites antud pinnast veel
ühe joonise, kuid teise nurga alt vaadatuna.
In[4]:=
Plot3D[ Sin[x] Sin[3y], {x,-2,2}, {y,-2,2},
PlotPoints->{25,25},
AxesLabel->{"x","y","z"},
ViewPoint->{-2.5,-1,2}]
PlotRange->{{xmin
,xmax},{ymin
,ymax},{zmin
,zmax}}
Võimaldab täpsustada, milline ruumi osa joonisel kujutatakse.
Oluline erinevus võrreldes vastava kahemõõtmelise
graafika parameetriga on see, et ruumigraafika korral lühike kirjaviis
PlotRange->{zmin ,zmax}
annab piirid
z-telje jaoks. Teiste sõnadega, nii saab määrata,
milliseid z-telje punkte läbivad joonise põrand ja
lagi.
2.2. Parameetriliste võrranditega antud funktsiooni graafik
Lisaks kahe muutuja funktsiooni graafikule on võimalik joonestada
ka keerukamaid pindu ja ruumijooni. Selleks kasutatakse käsku
ParametricPlot3D.
ParametricPlot3D[ {x(u; v),y(u;
v),z(u;
v)},
{u,umin,umax},
{v,vmin,vmax}]
Joonestab
ruumilise pinna parameetriliste võrranditega
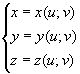 ,
kus u
Î [umin
;
umax]
ja v Î [vmin ;
vmax].
,
kus u
Î [umin
;
umax]
ja v Î [vmin ;
vmax].
ParametricPlot3Dga kasutatavad parameetrid erinevad mõnel
määral Plot3D juures nimetatutest. Näiteks puudub
parameetrid HiddenSurface, samuti tuleb arvestada, et PlotPoints
määrab
alajaotuste arvu
u ja v jaoks.
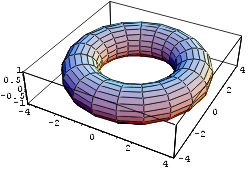
Näide 5. Joonestame toori parameetriliste võrranditega
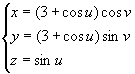 , kui u
Î
[0;2p ] ja
v Î
[0;2p ].
, kui u
Î
[0;2p ] ja
v Î
[0;2p ].
In[5]:=
ParametricPlot3D[
{(3+Cos[u])Cos[v], (3+Cos[u])Sin[v], Sin[u]},
{u,0,2 Pi},{v,0,2 Pi}]
ParametricPlot3D[ {x(t),y(t),z(t)},
{t,tmin,tmax}]
Joonestab ruumijoone parameetriliste võrranditega
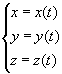 , kus t
Î
[tmin ; tmax].
, kus t
Î
[tmin ; tmax].
Ruumijoone joonestamisel võetakse alajaotuspunkte vaikimisi
75, kuid seda arvu saab muuta parameetri PlotPoints abil.
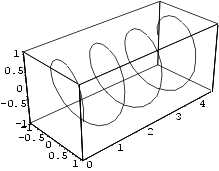
Näide 6. Joonestame kruvijoone, mille võrrandid
on
x = cos t, y = 0,2 t ja z = sin t,
ning
t
Î [0; 2p
]. Ilusama joonise saamiseks muudame parameetri ViewPoint väärtust.
In[6]:=
ParametricPlot3D[ {Cos[t], 0.2 t, Sin[t]},
{t,0,7 Pi},
ViewPoint->{2.15,-1.99,1.68}]
Eelmine
peatükk
Järgmine
peatükk
Sisukord








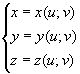 ,
kus u
Î [umin
;
umax]
ja v Î [vmin ;
vmax].
,
kus u
Î [umin
;
umax]
ja v Î [vmin ;
vmax].
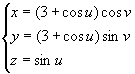 , kui u
Î
[0;2p ] ja
v Î
[0;2p ].
, kui u
Î
[0;2p ] ja
v Î
[0;2p ].

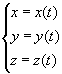 , kus t
Î
[tmin ; tmax].
, kus t
Î
[tmin ; tmax].
