Esimeses peatükis antakse Mathematica kasutamiseks vajalikud
algteadmised ja selgitatakse mõisteid, mida hilisemas töös
tarvis läheb. Et siia on püütud koondada vastuseid paljudele
võimalikele küsimustele, võib osa materjali algul tunduda
igav ja mittevajalik. Põhimõtteliselt võib lugeja
alustada juhendiga tutvumist oma jaoks kõige huvitavamast teemast,
kuid sel juhul võib-olla hiljem esimese peatüki juurde tagasi
pöörduda.
§1. KUIDAS TÖÖTAB MATHEMATICA
1.1. Töö alustamine
Mathematica käivitamisel avatakse automaatselt ka uus tööfail,
seetõttu võib kohe pärast paketi avanemist sisestada
esimese ülesande.
Sisestame klaviatuuril näiteks 1+2+3 .
Seejärel vajutame ühekorraga klahve [Shift] ja [Enter]. Ühe
sõrmega vajutatakse [Shift]-klahv alla ja teisega tehakse lühike
vajutus [Enter]-klahvile. (Te ei usu, kui palju probleeme tekitab selline
operatsioon algajatele!) Sellega anname märku, et ülesanne on
sisestatud ja arvuti võib seda lahendama hakata. Tulemus näeb
ekraanil välja järgmine:
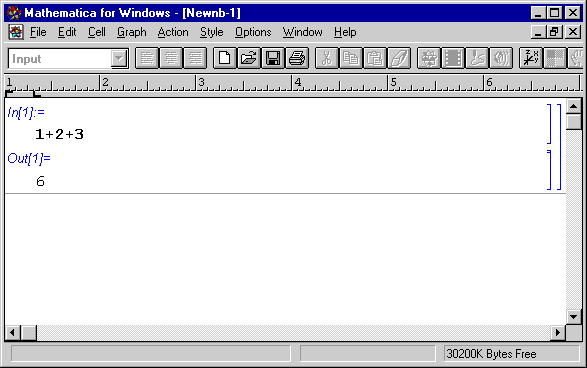
Kiri In[1] tähistab sisendrida ning Out[1] temale vastavat
väljundrida. Number 1 näitab, et see oli käesoleva töösessiooni
esimene arvutus. Mathematica annab kõigile arvutusele automaatselt
järjenumbri. Nummerdamist alustatakse 1-st iga kord peale paketi käivitamist.
Nii sisend- kui väljundrida on piiritletud akna paremas servas
paiknevate klambritega. Kolmas pikem klamber grupeerib sisend- ja väljundrea
üheks tervikuks.
Peenike must joon väljundrea järel on tegelikult kursor,
mis näitab järjepunkti asukohta. Uue ülesande sisestamisel
asendub joon tavalise tekstikursoriga.
1.2. Mathematica avaldise koostamine
Selleks, et Mathematica abil ülesannet lahendada, tuleb ülesanne
sõnastada sellele paketile arusaadavate väljendite abil. Seda
nimetatakse Mathematica avaldise koostamiseks. Kuna erinevaid võtmesõnu
on küllaltki palju ja süntaksireeglite poolt pakutavad võimalused
laialdased, võib avaldise koostamine keerukamate ülesannete
lahendamiseks olla väga komplitseeritud.
Esitame siinkohal mõned esmavajalikud põhitõed.
-
Tehtemärkidena kasutatakse arvutiasjanduses
üldlevinud sümboleid: + , , * ,
/ ja ^. Tehete järjekorda saab muuta ümarsulgude
abil.
Näide 1. Arvutame avaldise 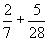 väärtuse.
väärtuse.
In[2]:= 2/7+5/28
Out[2]= 13
--
28
Väljundreal esitatakse harilik murd horisontaalse murrujoone abil
ja astendajad paigutatakse põhireast kõrgemale.
-
Kui ülesanne sisaldab tähti (muutujaid), siis toimitakse
nendega algebra reeglite järgi.
Näide 2. Arvutame avaldise 3a + 2a 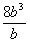 väärtuse.
väärtuse.
In[3]:= 3*a
+ 2*a - 8*b^3/b
Out[3]=
2
5 a - 8 b
-
Kümnendmurru komakohad eraldatakse punktiga. Kui arvu täisosa
on null, võib selle kirjutamata jätta. Näiteks arv 0,34
esitatakse kujul .34 . Harilikud murrud kirjutatakse jagamismärgi
abil.
-
Mathematica eristab täpseid ja ligikaudseid arve. Ligikaudse
arvu tunnuseks on arvus esinev kümnendpunkt. Seega kõik kümnendmurrud
on ligikaudsed arvud. Üldiselt püütakse vastused esitada
täpsete arvudena.
Näide 3. Proovime arvutada jagatise 123 : 56 väärtust.
In[4]:= 123/56
Out[4]= 123
---
56
Saadud tulemus on täiesti täpne, aga antud juhul kasutu.
-
Kui avaldis sisaldab kasvõi üht kümnendpunktiga arvu,
siis loobutakse täpsete arvude kasutamisest ja esitatakse tulemus
ligikaudse arvuna. Üldjuhul antakse vastus 6 tüvenumbriga. Selleks,
et leida jagatise 123/56 ligikaudset väärtust, tuleks ühele
arvudest lisada kümnendpunkt.
In[5]:= 123./56
Out[5]= 2.19643
-
Enamuse elementaarfunktsioonide jaoks on olemas spetsiaalsed väljendid
(näiteks Sin, Cos, Log). Funktsiooni argument asetatakse
kandilistesse sulgudesse.
Näide 4. Arvutame sin 0,2.
In[6]:= Sin[0.2]
Out[6]= 0.198669
-
Mathematica teeb ranget vahet suurte ja väikeste tähtede
vahel. Üldiselt on sisseehitatud väljendites esimene täht
suur ja järgnevad väikesed; liitsõnalistes väljendites
algab iga sõna suure tähega (näiteks ArcSin,
ViewPoint).
Kasutaja poolt defineeritud muutujad, funktsioonid jms. ei tarvitse seda
traditsiooni järgida.
-
Suure osa võtmesõnadest moodustavad käsud mitmesuguste
ülesannete lahendamiseks. On olemas käsud selleks, et lahendada
võrrandit, selleks, et joonestada funktsiooni graafikut ja selleks,
et leida funktsiooni tuletist. Edaspidi kasutame mõiste käsk
asemel vahel ka mõistet korraldus ja vahel mõistet operaator,
kui see on matemaatiliselt põhjendatud (näiteks tuletise leidmisel).
Tüüpiline Mathematica käsu kirjapilt on selline:
TeeMidagi[selleavaldisega]
Näide 5. Olgu meil avaldis (a + b + c)2
. Leiame avaldise lahtikorrutatud kuju, kasutades sulgude avamise käsku
Expand.
In[7]:= Expand[(a+b+c)^2]
Out[7]= 2
2
2
a + 2 a b + b + 2 a
c + 2 b c + c
-
Mathematica poolt arvutustele antavad reanumbrid võimaldavad
kasutada varem saadud tulemusi ilma neid uuesti klaviatuurilt sisestamata.
%n n-ndal real saadud tulemus;
% eelmisel real saadud tulemus;
%% üle-eelmisel real saadud tulemus.
Näide 6. Liidame 5. ja 6. real saadud tulemused, s. t. arvutame
2,19643 + 0,198669.
In[8]:= %5+%6
Out[8]= 2.3951
-
Muutujatele väärtuste omistamine toimub võrdusmärgi
abil.
Näide 7. Anname muutujale a väärtuse 3.
In[9]:= a = 3
Out[9]= 3
Omistame muutujatele x, y ja z väärtuse
1. Siin võib kasutada korduvat võrdust.
In[10]:= x = y = z = 1
Out[10]= 1
Muutuja väärtust saab tühistada, andes talle väärtuseks
punkti.
In[11]:= x=.
Arvutame nüüd avaldise a + 2x.
In[12]:= a + 2x
Out[12]= 3 + 2x
Muutuja a asendati tema väärtusega 3, x aga jääb
x-ks,
sest tema väärtuse tühistasime eelmisel real.
-
Ühele sisendreale võib kirjutada mitu erinevat avaldist;
sel juhul tuleb avaldised eraldada semikooloniga.
In[13]:= 12*3; a=6*6;
b=52/4
Out[13]= 13
Ekraanile väljastatakse ainult viimase avaldise väärtus,
kuid arvutused tehakse kõikide sisendrea avaldiste jaoks. Küsime
näiteks muutuja a väärtust:
-
Üldiselt, kui avaldise lõpus on semikoolon, siis tehakse kõik
arvutused, kuid tulemust ekraanile ei trükita.
1.3. Üldteadmisi Mathematica kasutamisest
-
Mathematica avaldise sisestamine ei erine üldiselt tööst
lihtsa tekstiredaktoriga. Kopeerimise, lõikamise ja liimimise käsud
paiknevad Edit-menüüs.
-
Teksti märgistamisel on aga üks oluline lisavõimalus:
kui teha hiireklõps mõnel ekraani paremas servas asuval klambril,
muutub klamber mustaks ja sellega on ka vastav rida märgistatud. See
on ainus võimalus mitme rea üheaegseks valimiseks. Mittevajaliku
rea täielikuks kustutamiseks tuleb samuti märgistada vastav klamber
ja siis vajutada klahvile [Delete] .
-
Mathematicas puudub automaatne ridade poolitamine. Selleks,
et pikemad avaldised tervenisti ekraanile mahuksid, tuleks paigutada nad
mitmele reale. Uuele reale minekuks vajutatakse klahvi [Enter]. Vajutus
sellele klahvile kutsub esile üksnes reavahetuse, kuid mitte ülesande
lahendamist, mida teatavasti tegi klahvikombinatsioon [Shift] + [Enter]
.
-
Kui arvutusprotsess venib pikale ja on alust kahtlustada, et sisendavaldises
on viga, oleks mõistlik arvutused katkestada. Selleks kasutatakse
klahvikombinatsiooni [Alt] + [.] ( [Alt] ja punkt).
-
Mathematica vajab tööks küllalt palju operatiivmälu.
Kuna kõigi antud töösessiooni jooksul tehtud arvutuste
tulemused säilitatakse, siis arvutuste lisandudes väheneb ka
kasutada oleva mälu hulk. Vaba mälu suurust näitab ekraani
alumises paremas servas olev indikaator. Kui indikaatori näit langeb
alla 1000 kilobaidi, oleks mõistlik töö salvestada, Mathematica
sulgeda ning seejärel uuesti avada.
-
Failide salvestamise, avamise ja sulgemise standardsed korraldused
paiknevad failimenüüs. Mathematicaga töötamisel
tuleb kokku puutuda põhiliselt kahte sorti failidega.
-
1. Tööfail ehk notebook. Tööfailides hoitakse
ülesandeid ja nende lahendusi, jooniseid. Failinime laiendiks on .ma
(see laiend pannakse salvestamisel automaatselt). Tavaliselt luuakse tööfaili
salvestamisel samasse kataloogi ka teine fail samasuguse nimega, kuid laiendiga
.mb
. Selleks, et notebooki hiljem avada, läheb tarvis ainult
.ma-laiendiga
faili. Kui salvestamise ruumi on vähe, võib
.mb-failid
kustutada.
Tavaliselt on notebook fail, kuhu kasutaja salvestab oma poolelijäänud
arvutused, et neid hiljem tarvitada. Teine osa notebooke luuakse
õppe- ja/või demonstratsiooni eesmärgil. Sellise faili
sisu on tavaliselt hoolikalt läbi mõeldud ja kommentaaridega
varustatud.
-
2. Programmifail ehk package. Neid kasutatakse programmide säilitamiseks.
Failinime laiendiks on .m . Et faili saaks programmina salvestada,
peab tal olema teatud kindel struktuur.
-
Mathematica jooniseid saab eraldi salvestada nii vektor- kui rastergraafika
failidena. Selleks tuleb soovitud joonis või joonise klamber hiirega
märgistada ja valida failimenüüst korraldus SaveAs.
Failitüübiks tuleb vektorgraafika jaoks valida .wmf
ja rastergraafika jaoks .bmp . Jooniseid saab eksportida ka lõikepuhvri
(clipboard) abil.
§2. TEHTED. KONSTANDID.
FUNKTSIOONID
2.1. Tehted
Aritmeetiliste tehete tegemisel võib kasutada tehtemärke, kuid
olemas on ka tehtele vastavad sõnalised operaatorid.
x+y+z
Plus[x,y,z] liitmine
-y
Minus[y]
lahutamine, negatiivne arv
x*y*z või x y z Times[x,y,z]
korrutamine
x/y
Devide[x,y] jagamine, harilik murd
x^y
Power[x,y] astendamine
Korrutamismärgina võib kasutada tühikut. Kui ei teki võimalust
mitmeseks tõlgendamiseks, võib ka tühiku ära jätta.
Näiteks võib kirjutada 4(2+3) , 3Sin[2] jne.
Avaldis 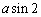 tuleb kirjutada kujul a Sin[2] ja mitte aSin[2], sest
viimasel juhul aSin omaette väljendiks.
tuleb kirjutada kujul a Sin[2] ja mitte aSin[2], sest
viimasel juhul aSin omaette väljendiks.
Tehtemärkide +, -, * ja /
ette ja järele võib lisada tühikuid, et muuta avaldist
paremini loetavaks. Näiteks x+y+z asemel võib kirjutada
x + y + z.
Kõigepealt tehakse astendamised, siis korrutamised ja jagamised
ning lõpuks liitmised ja lahutamised. Tehete järjekorda saab
muuta ümarsulgude abil.
Kui avaldis sisaldab harilikke murde, tuleb sageli kasutada täiendavaid
ümarsulge, mida traditsioonilise murrujoonega kirjaviisi korral pole
tarvis.
Näide 1.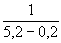
1/(5.2-0.2) ---> 0.2
1/(5.2-0.2) ---> 0.2
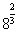
8^(2/3) ---> 4
8^(2/3) ---> 4
Mõnel juhul on lubatud kahe tehtemärgi kõrvutikirjutamine.
Näide 2.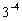 3^-4 --->
3^-4 ---> 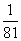
2 ( 3) 2*-3
---> -6
(Siin korrutamismärgina tühikut kasutada ei tohi.)
2.2. Konstandid
Sagedamini esinevate konstantide tähistamiseks on olemas spetsiaalsed
väljendid.
Pi
p
E
e
I
i = 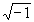
Degree
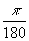 (1 kraad)
(1 kraad)
Infinity ¥
(lõpmatus)
Konstantidega võib teha tehteid nii nagu arvudega. Konstant
loetakse täpseks arvuks, seega Pi + 2Pi annab tulemsueks
3Pi,
aga mitte 9.42478. Vajaduse korral esitab Mathematica ka
ülesande vastuse konstantide abil.
Näide 3. Arvutame kahe kompleksarvu jagatise 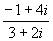 .
.
In[1]:=
(-1+4I)/(3+2I)
Out[1]=
5 14 I
-- + ----
13 13
2.3. Funktsioonid
Kuna meie vaadeldav tarkvarapakett on loodud spetsiaalselt matemaatiliste
ülesannete lahendamiseks, siis on talle sisse ehitatud võrdlemisi
suur hulk matemaatilisi funktsioone. Käesolevas punktis vaatleme neist
tuntumaid. Funktsiooni argument esitatakse enamasti kandilistes sulgudes.
Kui argumente on mitu, siis eraldatakse nad komadega.
-
Mõned tuntumad elementaarfunktsioonid on järgmised:
Sqrt[x] ruutjuur 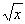
Log[x] naturaallogaritm x-st ln x
Log[a,x] logaritm x-st alusel a logax
Exp[x] eksponentfunktsioon ex
-
Trigonomeetrilised ja hüperboolsed funktsioonid ning nende pöördfunktsioonid
esitame tabelina. Trigonomeetriliste funktsioonide korral esitatakse argument
radiaanides.
| |
Trigonomeetrilised funktsioonid
|
Arkusfunktsioonid
|
Hüperboolsed funktsioonid
|
Areafunktsioonid
|
| Siinus |
Sin[x]
|
ArcSin[x]
|
Sinh[x]
|
ArcSinh[x]
|
| Koosinus |
Cos[x]
|
ArcCos[x]
|
Cosh[x]
|
ArcCosh[x]
|
| Tangens |
Tan[x]
|
ArcTan[x]
|
Tanh[x]
|
ArcTanh[x]
|
| Kootangens |
Cot[x]
|
ArcCot[x]
|
Coth[x]
|
ArcCoth[x]
|
| Seekans |
Sec[x]
|
ArcSec[x]
|
Sech[x]
|
ArcSech[x]
|
| Kooseekans |
Csc[x]
|
ArcCsc[x]
|
Csch[x]
|
ArcCsch[x]
|
Näide 4. Arvutame tan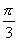 täpse väärtuse.
täpse väärtuse.
In[2]:=
Tan[Pi/3]
Out[2]=
Sqrt[3]
Tulemuseks
saime 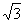 .
.
Näide 5. Arvutame 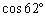 väärtuse kümnendmurruna. Kuna argument on antud kraadides,
korrutame ta konstandiga Degree. Et saada tulemust kümnendmurruna,
kasutame funktsiooni N, mida kirjeldame pisut allpool.
väärtuse kümnendmurruna. Kuna argument on antud kraadides,
korrutame ta konstandiga Degree. Et saada tulemust kümnendmurruna,
kasutame funktsiooni N, mida kirjeldame pisut allpool.
In[3]:=
N[Cos[62
Degree]]
Out[3]=
0.469472
Lisaks matemaatilisest analüüsist tuntud funktsioonidele
esineb ka rida teisi funktsioone, mida tavaliselt funktsioonideks ei nimetata.
Sellised on näiteks avaldise ligikaudse väärtuse leidmine,
ümardamine, ühisteguri leidmine, juhuarvude genereerimine jne.
-
Üht võimalust avaldise ligikaudse väärtuse arvutamiseks
näitasime punktis 1.1.2. Teine võimalus on kasutada spetsiaalset
funktsiooni N.
N[ avaldis ] Arvutab avaldise
ligikaudse väärtuse 6 tüvenumbriga.
N[ avaldis,n ]
Arvutab avaldise ligikaudse väärtuse n tüvenumbriga.
Näide 6. Leiame 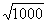 väärtuse 20 tüvenumbriga.
väärtuse 20 tüvenumbriga.
In[4]:=
N[Sqrt[1000],20]
Out[4]=
31.62277660168379332
-
Arvude ümardamiseks ja täisosa leidmiseks on olemas järgmised
funktsioonid:
Round[x] Ümardab
x-i,
annab x-le lähima täisarvu.
Näide 7. Round[2.4] ---> 2
Round[2.6] ---> 3
Round[-2.4]
---> -2 Round[-2.6] ---> -3
Floor[x] Annab suurima
täisarvu, mis on x-st väiksem või temaga võrdne.
Teiste sõnadega, leiab x täisosa ehk entier x.
Näide 8. Floor[2.4] ---> 2
Floor[2.6] ---> 2
Floor[-2.4] ---> -3
Floor[-2.6] ---> -3
Ceiling[x] Annab väikseima
täisarvu, mis on x-st suurem või temaga võrdne.
Näide 9. Ceiling[2.4] ---> 3
Ceiling[2.6] ---> 3
Ceiling[-2.4] ---> -2
Ceiling[-2.6] ---> -2
-
Suurima ühisteguri ja vähima ühiskordse leidmine:
GCD[n1, n2,
]
Leiab
täisarvude n1, n2,
suurima ühisteguri.
Näide 10. Leiame arvude 9, 12 ja 21 suurima ühisteguri.
GCD[9,12,21] ---> 3
LCM[n1, n2,
]
Leiab täisarvude n1,
n2,
vähima
ühiskordse.
Näide 11. Leiama arvude 6, 18, 72 ja 108 vähima ühiskordse.
LCM[6,18,72,108]
---> 216
-
Juhuarvude genereerimiseks kasutatakse järgmisi funktsioone:
Random[] Annab pseudojuhuarvu piirkonnas [0;
1].
Random[arvutüüp,{xmin
,xmax}]
Annab määratud tüüpi pseudojuhuarvu piirkonnas [xmin;
xmax].
Võimalikud arvutüübid on Integer,
Real
ja Complex.
SeedRandom[n] Juhuslike
arvude generaatori uus laadimine, kusjuures täisaarv n määrab
arvutuse algväärtuse.
SeedRandom[] Siin kasutatakse arvutuse algväärtuse
jaoks kellaaega.
-
Faktoraali arvutamiseks võib kasutada hüüumärki,
kuid on olemas ka vastav võtmesõna.
n! ehk Factorial[n]
faktoriaal
n! = n·(n 1)·(n
2)·
·2·1
n!! ehk Factorial2[n]
poolfaktoriaal
n!! = n·(n 2)·(n
4)·
.
-
Funktsioonid reaalarvu märgi ja absoluutväärtuse leidmiseks
ning funktsioonid kompleksarvu mooduli, argumendi, reaalosa ja imaginaarosa
leidmiseks:
Sign[x] märgifunktsioon,
sign x = 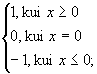
Abs[x] reaalarvu korral
arvu x absoluutväärtus; kompleksarvu korral arvu x
moodul;
Arg[z] kompleksarvu z
argument;
Re[z] kompleksarvu z
reaalosa;
Im[z] kompleksarvu z
imaginaarosa.
Näide 12. Arvutame kompleksarvu 3 + 2i
mooduli.
In[5]:= Abs[-4+2
I]
Out[5]= 2 Sqrt[5]
Tulemuseks saime 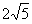 .
.
§3. LOENDID
3.1. Loendi mõiste
Loend (list) kujutab endast avaldiste jada, mis on omavahel komadega eraldatud
ja paigutatud loogelistesse sulgusesse. Tüüpiline loend on näiteks
{a,b,c,d,e,f}.
Ühetüübiliste andmete loendisse grupeerimine muudab
esituse ülevaatlikumaks ja kompaktsemaks, seda nii arvuti kui inimese
seisukohalt. Loendeid võib vaadelda kui matemaatikas kasutatavate
vektorite ja maatriksite analooge. Programmeerimises nimetatakse selliseid
andmetervikuid tavaliselt massiivideks.
-
{a,b,c} vektor (a; b; c) ehk ühemõõtmeline
loend. Sageli kasutame ka nimetust ühemõõtmeline massiiv
või ühedimensionaalne massiiv.
Loendist ühe elemendi eraldamiseks kirjutatakse loendi järele
elemendi järjenumber kahekordsetes kandilisetes sulgudes.
Näide 1. Küsime loendi (20; 30; 40; 50) teise
elemendi väärtust.
In[1]:= {20,30,40,50}[[2]]
Out[1]= 30
Negatiivse järjenumbri korral loendatakse elemente loendi lõpust
alates.
In[2]:= {a,2a,3a,4a,5a}[[-1]]
Out[2]= 5 a
-
Kui ühemõõtmelise loendi iga element on omakorda loend,
saame kahemõõtmelise loendi. Loendit {{a1,a2,a3},{b1,b2,b3},{c1,c2,c3}}
võib vaadelda maatriksina
Kui maatriksis on palju ridu ja veerge, on mõistlik tema väljastamisel
kasutada käsku TableForm, mis paigutab elemendid tabelikujuliselt.
Näide 2. Olgu meil maatriks m = 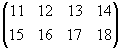
In[3]:= m
= {{11,12,13,14},{15,16,17,18}}
Out[3]= {{11,
12, 13, 14}, {15, 16, 17, 18}}
In[4]:= TableForm[m]
Out[4]= 11
12 13 14
15 16 17 18
Kahemõõtmelise loendi elemendid on omakorda loendid.
Küsides loendi m teise elemendi väärtust, saame maatriksi
teise rea.
In[5]:= m[[2]]
Out[5]= {15, 16,
17, 18}
Mitmemõõtmelisest loendist üksiku elemendi eraldamiseks
on kaks samaväärset võimalust. Küsime maatriksi m
teise rea kolmanda elemendi väärtust.
In[6]:= m[[2,3]]
Out[6]= 17
In[7]:= m[[2]][[3]]
Out[7]= 17
-
Võimalikud on ka kolme ja enamamõõtmelised loendid.
3.2. Tehted loenditega
-
Kui kahe võrdse pikkusega loendi vahele asetada mingi tehtemärk,
on tulemuseks loend, mille elemendid on saadud tehte rakendamisel lähteloendite
vastavatele elementidele. Kuna tehtemärk kahe loendi vahel võib
olla suvaline, on tehniliselt täiesti teostatav ka loendite jagamine
ja astendamine, kuigi viimased operatsioonid ei ole aritmeetiliste vektorite
(maatriksite) puhul mõeldavad.
Näide 3. Liidame kaks ühemõõtmelist
loendit (vektorit).
In[8]:= {a,b,c} +
{d,e,f}
Out[8]= {a + d, b + e,
c + f}
Tulemus on kooskõlas aritmeetiliste vektorite liitmise reegliga.
Näide 4. Korrutame omavahel kaks loendit (vektorit).
In[9]:=
{1,2,3}*{4,5,6}
Out[9]=
{4, 10, 18}
NB! Tulemuseks saadud vektor ei ole korrutatud vektorite skalaarkorrutis
ega ka nende vektorkorrutis, vaid tegurite vastavate elementide korrutamisel
saadud vektor.
-
Kui asetada tehtemärk loendi ja üksiku avaldise vahele, saame
tulemuseks loendi, mille elemendid on saadud tehte rakendamisel loendi
vastavatele elementidele ja eraldiseisvale avaldisele.
Näide 5. Korrutame arvu 3 ja loendi {1,2,3,4}.
In[10]:= 3*{1,2,3,4}
Out[10]= {3, 6, 9,
12}
Tulemus on aritmeetilise vektori korrutis skalaariga.
Näide 6. Liidame arvule 3 loendi {1,2,3,4}.
In[11]:=
3 + {1,2,3,4}
Out[11]=
{4, 5, 6, 7}
Aritmeetilist vektorit ja arvu selliselt liita ei tohi, kuid abstraktse
loendi korral on see tehe korrektne.
-
Kahe vektori x ja y skalaarkorrutise leidmiseks kirjutatakse
nende vahele tehtemärgina punkt. Vastav sõnaline operaator
on Dot[x,y]. Samal viisil saab
leida kahe maatriksi korrutist.
Näide 7. Arvutame vektorite (2; 3; 5 ) ja ( 4;
0; 12 ) skalaarkorrutise.
In[12]:= {2,-3,5}.{-4,0,12}
Out[12]= 52
3.3. Loendite koostamine
Loendite abil on lihtne lahendada funktsioonide tabuleerimisega seotud
ülesandeid. Üks lihtsamaid võimalusi vajaliku loendi koostamiseks
on korraldus Table.
Table[f(i),{i,imax
}]
Tulemuseks saame loendi {f(1),f(2),f(3),
,f(imax)}.
Koostatakse loend funktsiooni väärtustest, kui argument i
muutub 1-st kuni imax-ini sammuga 1.
Näide 8. Koostame loendi, mille elementideks on naturaalarvude
1 10 ruudud.
In[13]:=
Table[i^2,{i,10}]
Out[13]=
{1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
Käsul Table on olemas mitu erinevat süntaksivarianti.
Table[f(i),{i,imin
,imax
}]
Siin määratakse i algväärtuseks
imin.
Table[f(i),{i,imin
,imax
,di}]
Muutuja
i
väärtust muudetakse sammuga di.
Näide 9. Koostame funktsiooni f(x) =
3x3 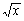 väärtuste tabeli piirkonnas [1; 2] sammuga 0,1.
väärtuste tabeli piirkonnas [1; 2] sammuga 0,1.
In[14]:=
TableForm[
Table[{x, 3*x^3-Sqrt[x]}, {x, 1, 2, 0.1}]
]
Out[14]//TableForm=
1 2
1.1 2.94419
1.2 4.08855
1.3 5.45082
1.4 7.04878
1.5 8.90026
1.6 11.0231
1.7 13.4352
1.8 16.1544
1.9 19.1986
2. 22.5858
Tulemuseks on kahemõõtmeline loend. Selles on võimalik
veenduda, kui jätta ära korraldus TableForm.
Table[f(i ; j ;
),{i,imin
,imax
,di},{j,jmin
,jmax
,dj},
]
Nii saab koostada mitmemõõtmelisi loendeid.
Näide 10. Koostame tabeli, mille esimses veerus oleksid
naturaalarvud 1 10, teises veerus nende ruudud, kolmandas kuubid ja viimases
neljandad astmed.
In[15]:= TableForm[Table[ i^j,
{i,10},{j,4}]]
Out[15]//TableForm=
1 1 1
1
2 4 8
16
3 9 27 81
4 16 64 256
5 25 125 625
6 36 216 1296
7 49 343 2401
8 64 512 4096
9 81 729 6561
10 100 1000 10000
Järgmine
peatükk Sisukord

täpse väärtuse.
![]() .
.
![]() väärtuse kümnendmurruna. Kuna argument on antud kraadides,
korrutame ta konstandiga Degree. Et saada tulemust kümnendmurruna,
kasutame funktsiooni N, mida kirjeldame pisut allpool.
väärtuse kümnendmurruna. Kuna argument on antud kraadides,
korrutame ta konstandiga Degree. Et saada tulemust kümnendmurruna,
kasutame funktsiooni N, mida kirjeldame pisut allpool.
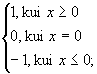

![]() väärtuste tabeli piirkonnas [1; 2] sammuga 0,1.
väärtuste tabeli piirkonnas [1; 2] sammuga 0,1.